
(1)1.72.5,1.73;(2)0.8-0.1,0.8-0.2;(3)1.70.3,0.93.1.
思路分析:利用單調性或中間變量.
解:(1)考查指數函數y=1.7x,由于底數1.7>1,
∴指數函數y=1.7x在(-∞,+∞)上是增函數.
∵2.5<3,∴1.72.5<1.73.
(2)考查函數y=0.8x,由于0<0.8<1,
∴指數函數y=0.8x在(-∞,+∞)上為減函數.
∵-0.1>-0.2,
∴0.8-0.1<0.8-0.2.
(3)由指數函數的性質得1.70.3>1.70=1,0.93.1<0.90=1.
∴1.70.3>0.93.1.
溫馨提示
(1)對于同底數冪,要利用相應指數函數的單調性,通過自變量的大小關系可以判斷相應函數值的大小.
(2)對于1.70.3與0.93.1,不能直接看成某一個指數函數的兩個值.所以(3)題無法用(1)、(2)兩題的方法來進行比較.本題可在這兩個數值間找到數值1.使這兩個數值分別與數值1進行比較,通過搭橋進而比較出1.70.3與0.93.1的大小.常插入的數值可能是0或±1.根據問題的實際也可能是其他數值.


 同步學典一課多練系列答案
同步學典一課多練系列答案 經典密卷系列答案
經典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案科目:高中數學 來源:同步題 題型:解答題
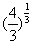 ,
,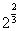 ,
, ,
,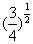 的大小。
的大小。查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com