
【題目】古希臘畢達(dá)哥拉斯學(xué)派研究了“多邊形數(shù)”,人們把多邊形數(shù)推廣到空間,研究了“四面體數(shù)”,下圖是第一至第四個(gè)四面體數(shù),(已知![]() )
)
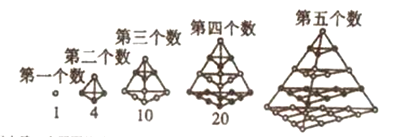
觀察上圖,由此得出第5個(gè)四面體數(shù)為______(用數(shù)字作答);第![]() 個(gè)四面體數(shù)為______.
個(gè)四面體數(shù)為______.
【答案】35 ![]()
【解析】
通過觀察圖形,先將圖形的規(guī)律轉(zhuǎn)化為數(shù)字規(guī)律,即為找到如1,4,10,20,……的數(shù)列的第![]() 項(xiàng),通過觀察發(fā)現(xiàn),相鄰的數(shù)字差分別是3,6,10,……,即第
項(xiàng),通過觀察發(fā)現(xiàn),相鄰的數(shù)字差分別是3,6,10,……,即第![]() 項(xiàng)應(yīng)為
項(xiàng)應(yīng)為![]() ,那么就把問題轉(zhuǎn)化為求數(shù)列
,那么就把問題轉(zhuǎn)化為求數(shù)列![]() 的和,
的和,![]() 為1,3,6,10,……,根據(jù)這些數(shù)字可以發(fā)現(xiàn),
為1,3,6,10,……,根據(jù)這些數(shù)字可以發(fā)現(xiàn),![]() ,
, ![]() ,……,
,……, ![]() ,利用累加法可以得到
,利用累加法可以得到![]() ,再利用題目所給已知,求出前
,再利用題目所給已知,求出前![]() 項(xiàng)和,即為第
項(xiàng)和,即為第![]() 個(gè)四面體數(shù),當(dāng)
個(gè)四面體數(shù),當(dāng)![]() 時(shí),即為第5個(gè)四面體數(shù).
時(shí),即為第5個(gè)四面體數(shù).
由題,
第一個(gè)四面體數(shù)為1;
第二個(gè)四面體數(shù)為![]() ;
;
第三個(gè)四面體數(shù)為![]() ;
;
第四個(gè)四面體數(shù)為![]()
……
由此可歸納,第![]() 個(gè)四面體數(shù)為
個(gè)四面體數(shù)為![]()
即為![]()
設(shè)該式中的每個(gè)數(shù)從左至右的排列為數(shù)列![]() ,即
,即![]() 為:1,3,6,10,……
為:1,3,6,10,……
得到遞推關(guān)系為![]() ,
,![]() ,…,
,…,![]() ,相加后得
,相加后得![]()
![]() ,故數(shù)列
,故數(shù)列![]() 的和
的和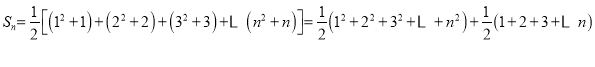
![]()
![]() 當(dāng)
當(dāng)![]() 時(shí),
時(shí),![]()
故答案為:35;![]()



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)求函數(shù)![]() 的最小正周期和單調(diào)遞減區(qū)間;
的最小正周期和單調(diào)遞減區(qū)間;
(2)將函數(shù)![]() 的圖象向右平移
的圖象向右平移![]() 個(gè)單位后,再將所得圖象的縱坐標(biāo)不變,橫坐標(biāo)伸長到原來的2倍,得到的函數(shù)
個(gè)單位后,再將所得圖象的縱坐標(biāo)不變,橫坐標(biāo)伸長到原來的2倍,得到的函數(shù)![]() 的圖象關(guān)于
的圖象關(guān)于![]() 軸對稱,求
軸對稱,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,且曲線
,且曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線與直線
處的切線與直線![]() 垂直.
垂直.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)求證:![]() 時(shí),
時(shí),![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】關(guān)于函數(shù)![]()
![]() ,有下列四個(gè)命題:①
,有下列四個(gè)命題:①![]() 的值域是
的值域是![]() ;②
;②![]() 是奇函數(shù);③
是奇函數(shù);③![]() 在
在![]() 上單調(diào)遞增;④方程
上單調(diào)遞增;④方程![]() 總有四個(gè)不同的解;其中正確的是( )
總有四個(gè)不同的解;其中正確的是( )
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】![]() 紙是生活中最常用的紙規(guī)格.
紙是生活中最常用的紙規(guī)格.![]() 系列的紙張規(guī)格特色在于:①
系列的紙張規(guī)格特色在于:①![]() 、
、![]() 、
、![]() 、…、
、…、![]() ,所有尺寸的紙張長寬比都相同.②在
,所有尺寸的紙張長寬比都相同.②在![]() 系列紙中,前一個(gè)序號(hào)的紙張以兩條長邊中點(diǎn)連線為折線對折裁剪分開后,可以得到兩張后面序號(hào)大小的紙,比如1張
系列紙中,前一個(gè)序號(hào)的紙張以兩條長邊中點(diǎn)連線為折線對折裁剪分開后,可以得到兩張后面序號(hào)大小的紙,比如1張![]() 紙對裁后可以的到2張
紙對裁后可以的到2張![]() 紙,1張
紙,1張![]() 紙對裁可以得到2張
紙對裁可以得到2張![]() 紙,以此類推.這是因?yàn)?/span>
紙,以此類推.這是因?yàn)?/span>![]() 系列的紙張長寬比為
系列的紙張長寬比為![]() 這一特殊比例,所以具備這種特性.已知
這一特殊比例,所以具備這種特性.已知![]() 紙規(guī)格為84.1厘米×118.9厘米(
紙規(guī)格為84.1厘米×118.9厘米(![]() ).那么
).那么![]() 紙的長度為( )
紙的長度為( )
A.14.8厘米B.21厘米C.25.1厘米D.29.7厘米
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)準(zhǔn)備招聘一批大學(xué)生到本單位就業(yè),但在簽約前要對他們的某項(xiàng)專業(yè)技能進(jìn)行測試.在待測試的某一個(gè)小組中有男、女生共10人(其中女生人數(shù)多于男生人數(shù)),如果從中隨機(jī)選2人參加測試,其中恰為一男一女的概率為![]() ;(Ⅰ)求該小組中女生的人數(shù);(Ⅱ)假設(shè)此項(xiàng)專業(yè)技能測試對該小組的學(xué)生而言,每個(gè)女生通過的概率均為
;(Ⅰ)求該小組中女生的人數(shù);(Ⅱ)假設(shè)此項(xiàng)專業(yè)技能測試對該小組的學(xué)生而言,每個(gè)女生通過的概率均為![]() ,每個(gè)男生通過的概率均為
,每個(gè)男生通過的概率均為![]() ;現(xiàn)對該小組中男生甲、男生乙和女生丙3個(gè)人進(jìn)行測試,記這3人中通過測試的人數(shù)為隨機(jī)變量
;現(xiàn)對該小組中男生甲、男生乙和女生丙3個(gè)人進(jìn)行測試,記這3人中通過測試的人數(shù)為隨機(jī)變量![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的右焦點(diǎn)為
的右焦點(diǎn)為![]() ,長半軸長與短半軸長的比值為
,長半軸長與短半軸長的比值為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)經(jīng)過點(diǎn)![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于不同的兩點(diǎn)
相交于不同的兩點(diǎn)![]() ,
,![]() .若點(diǎn)
.若點(diǎn)![]() 在以線段
在以線段![]() 為直徑的圓上,求直線
為直徑的圓上,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖![]() ,在梯形
,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() 是
是![]() 與
與![]() 的交點(diǎn),將
的交點(diǎn),將![]() 沿
沿![]() 翻折到圖
翻折到圖![]() 中
中![]() 的位置,得到四棱錐
的位置,得到四棱錐![]() .
.

(1)求證:![]() ;
;
(2)當(dāng)![]() ,
,![]() 時(shí),求
時(shí),求![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() 為
為![]() 的導(dǎo)函數(shù).
的導(dǎo)函數(shù).
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)![]() 在
在![]() 上存在最大值0,求函數(shù)
上存在最大值0,求函數(shù)![]() 在
在![]() 上的最大值;
上的最大值;
(3)求證:當(dāng)![]() 時(shí),
時(shí),![]() .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com