【題目】已知橢圓
，其焦距為2，離心率為
（1）求橢圓
的方程；
（2）設橢圓的右焦點為
， 
為
軸上一點，滿足
，過點
作斜率不為0的直線
交橢圓于
兩點，求
面積
的最大值.
能考試期末沖刺卷系列答案科目：高中數學 來源： 題型：
【題目】設函數
， 
（
）.
（1）當
時，若函數
與
的圖象在
處有相同的切線，求
的值；
（2）當
時，若對任意
和任意
，總存在不相等的正實數
，使得
，求
的最小值；
（3）當
時，設函數
與
的圖象交于
兩點．求證： 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2017年4月1日,新華通訊社發布:國務院決定設立河北雄安新區.消息一出,河北省雄縣、容城、安新3縣及周邊部分區域迅速成為海內外高度關注的焦點.
(1)為了響應國家號召,北京市某高校立即在所屬的8個學院的教職員工中作了“是否愿意將學校整體搬遷至雄安新區”的問卷調查,8個學院的調查人數及統計數據如下:
調查人數( | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
愿意整體搬遷人數( | 8 | 17 | 25 | 31 | 39 | 47 | 55 | 66 |
請根據上表提供的數據,用最小二乘法求出變量
關于變量
的線性回歸方程
保留小數點后兩位有效數字);若該校共有教職員工2500人,請預測該校愿意將學校整體搬遷至雄安新區的人數;
(2)若該校的8位院長中有5位院長愿意將學校整體搬遷至雄安新區,現該校擬在這8位院長中隨機選取4位院長組成考察團赴雄安新區進行實地考察,記
為考察團中愿意將學校整體搬遷至雄安新區的院長人數,求
的分布列及數學期望.
參考公式及數據: 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在四棱錐PABCD中，AD∥BC，平面PAC⊥平面ABCD，AB=AD=DC=1，
∠ABC=∠DCB=60，E是PC上一點.
（Ⅰ）證明：平面EAB⊥平面PAC；
（Ⅱ）若△PAC是正三角形，且E是PC中點，求三棱錐AEBC的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著共享單車的成功運營，更多的共享產品逐步走入大家的世界，共享汽車、共享籃球、共享充電寶等各種共享產品層出不窮.某公司隨機抽取
人對共享產品對共享產品是否對日常生活有益進行了問卷調查，并對參與調查的
人中的性別以及意見進行了分類，得到的數據如下表所示：
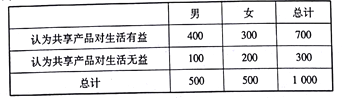
（Ⅰ）根據表中的數據，能否在犯錯的概率不超過
的前提下，認為對共享產品的態度與性別有關系？
（Ⅱ）為了答謝參與問卷調查的人員，該公司對參與本次問卷調查的人員隨機發放
張超市的購物券，購物券金額以及發放的概率如下：
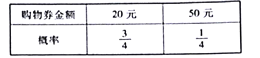
現有甲、乙兩人領取了購物券，記兩人領取的購物券的總金額為
，求
的分布列和數學期望.
參考公式： 
.
臨界值表：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知曲線
的參數方程為
，其中
為參數，且
在直角坐標系
中，以坐標原點
為極點，以
軸正半軸為極軸建立極坐標系.
（1）求曲線
的極坐標方程；
（2）設
是曲線
上的一點，直線
被曲線
截得的弦長為
，求
點的極坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
為坐標原點，拋物線
上在第一象限內的點
到焦點的距離為
，曲線
在點
處的切線交
軸于點
，直線
經過點且垂直于軸．
（Ⅰ）求點的坐標；
（Ⅱ）設不經過點和的動直線
交曲線于點
和
，交于點
，若直線
，
，
的斜率依次成等差數列，試問：
是否過定點？請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
