
【題目】若存在![]() 與正實(shí)數(shù)
與正實(shí)數(shù)![]() ,使得
,使得![]() 成立,則稱函數(shù)
成立,則稱函數(shù)![]() 在
在![]() 處存在距離為
處存在距離為![]() 的對稱點(diǎn),把具有這一性質(zhì)的函數(shù)
的對稱點(diǎn),把具有這一性質(zhì)的函數(shù)![]() 稱之為“
稱之為“![]() 型函數(shù)”.
型函數(shù)”.
(1)設(shè)![]() ,試問
,試問![]() 是否是“
是否是“![]() 型函數(shù)”?若是,求出實(shí)數(shù)
型函數(shù)”?若是,求出實(shí)數(shù)![]() 的值;若不是,請說明理由;
的值;若不是,請說明理由;
(2)設(shè)![]() 對于任意
對于任意![]() 都是“
都是“![]() 型函數(shù)”,求實(shí)數(shù)
型函數(shù)”,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)是,![]() ;(2)
;(2)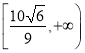 .
.
【解析】
(1)假設(shè)函數(shù)![]() 是“
是“![]() 型函數(shù)”,由定義得出
型函數(shù)”,由定義得出![]() ,經(jīng)過化簡計(jì)算出正實(shí)數(shù)
,經(jīng)過化簡計(jì)算出正實(shí)數(shù)![]() 的值即可;
的值即可;
(2)由題中定義得出![]() ,利用參變量分離法得出
,利用參變量分離法得出![]() ,利用雙勾函數(shù)的單調(diào)性求出
,利用雙勾函數(shù)的單調(diào)性求出![]() 在
在![]() 上的值域,即可得出實(shí)數(shù)
上的值域,即可得出實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
(1)假設(shè)函數(shù)![]() 是“
是“![]() 型函數(shù)”,由定義得出
型函數(shù)”,由定義得出![]() ,
,
![]() ,由
,由![]() ,得
,得![]() ,
,
則有![]() ,
,![]() ,化簡得
,化簡得![]() ,解得
,解得![]() .
.
因此,函數(shù)![]() 是“
是“![]() 型函數(shù)”;
型函數(shù)”;
(2)![]() 對于任意
對于任意![]() 都是“
都是“![]() 型函數(shù)”,
型函數(shù)”,
則![]() ,
,
即![]() ,
,
化簡得![]() ,即
,即![]() ,
,
由雙勾函數(shù)的單調(diào)性可知,函數(shù)![]() 在
在![]() 上是增函數(shù).
上是增函數(shù).
當(dāng)![]() 時,
時,![]() ,所以,
,所以,![]() ,解得
,解得![]() .
.
因此,實(shí)數(shù)![]() 的取值范圍是
的取值范圍是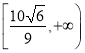 .
.


 名校課堂系列答案
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,邊長為![]() 的正方形
的正方形![]() 與梯形
與梯形![]() 所在的平面互相垂直,已知
所在的平面互相垂直,已知![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在線段
在線段![]() 上.
上.

(1)證明:平面![]() 平面
平面![]() ;
;
(2)判斷點(diǎn)![]() 的位置,使得平面
的位置,使得平面![]() 與平面
與平面![]() 所成的銳二面角為
所成的銳二面角為![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】圖(1)為東方體育中心,其設(shè)計(jì)方案側(cè)面的外輪廓線如圖(2)所示;曲線![]() 是以點(diǎn)
是以點(diǎn)![]() 為圓心的圓的一部分,其中
為圓心的圓的一部分,其中![]() ,曲線
,曲線![]() 是拋物線
是拋物線![]() 的一部分;
的一部分;![]() 且
且![]() 恰好等于圓
恰好等于圓![]() 的半徑,
的半徑,![]() 與圓相切且
與圓相切且![]() .
.
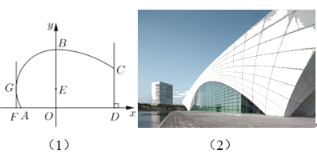
(1)若要求![]() 米,
米,![]() 米,求
米,求![]() 與
與![]() 的值;
的值;
(2)當(dāng)![]() 時,若要求
時,若要求![]() 不超過45米,求
不超過45米,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,橢圓
中,橢圓![]() 的右焦點(diǎn)為
的右焦點(diǎn)為![]() ,直線為
,直線為![]() .
.
(1)求到點(diǎn)![]() 和直線
和直線![]() 的距離相等的點(diǎn)
的距離相等的點(diǎn)![]() 的軌跡方程;
的軌跡方程;
(2)過點(diǎn)![]() 作直線交橢圓
作直線交橢圓![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() ,又直線
,又直線![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,若
,若![]() ,求線段
,求線段![]() 的長;
的長;
(3)已知點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,![]() ,直線
,直線![]() 交直線
交直線![]() 于點(diǎn)
于點(diǎn)![]() ,且和橢圓
,且和橢圓![]() 的一個交點(diǎn)為點(diǎn)
的一個交點(diǎn)為點(diǎn)![]() ,是否存在實(shí)數(shù)
,是否存在實(shí)數(shù)![]() ,使得
,使得![]() ?若存在,求出實(shí)數(shù)
?若存在,求出實(shí)數(shù)![]() ,若不存在,說明理由.
,若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】5張獎券中有2張是中獎的,先由甲抽1張,然后由乙抽1張,抽后不放回,求:
(1)甲中獎的概率![]() ;
;
(2)甲、乙都中獎的概率![]() ;
;
(3)只有乙中獎的概率![]() ;
;
(4)乙中獎的概率![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】將數(shù)列![]() 的前
的前![]() 項(xiàng)分成兩部分,且兩部分的項(xiàng)數(shù)分別是
項(xiàng)分成兩部分,且兩部分的項(xiàng)數(shù)分別是![]() ,若兩部分和相等,則稱數(shù)列
,若兩部分和相等,則稱數(shù)列![]() 的前
的前![]() 項(xiàng)的和能夠進(jìn)行
項(xiàng)的和能夠進(jìn)行![]() 等和分割.
等和分割.
(1)若![]() ,試寫出數(shù)列
,試寫出數(shù)列![]() 的前
的前![]() 項(xiàng)和所有等和分割;
項(xiàng)和所有等和分割;
(2)求證:等差數(shù)列![]() 的前
的前![]() 項(xiàng)的和能夠進(jìn)行
項(xiàng)的和能夠進(jìn)行![]() 等和分割;
等和分割;
(3)若數(shù)列![]() 的通項(xiàng)公式為:
的通項(xiàng)公式為:![]() ,且數(shù)列
,且數(shù)列![]() 的前
的前![]() 項(xiàng)的和能夠進(jìn)行等和分割,求所有滿足條件的
項(xiàng)的和能夠進(jìn)行等和分割,求所有滿足條件的![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)數(shù)列A:![]() ,
,![]() ,…
,…![]() (
(![]() ).如果對小于
).如果對小于![]() (
(![]() )的每個正整數(shù)
)的每個正整數(shù)![]() 都有
都有![]() <
<![]() ,則稱
,則稱![]() 是數(shù)列A的一個“G時刻”.記“
是數(shù)列A的一個“G時刻”.記“![]() 是數(shù)列A的所有“G時刻”組成的集合.
是數(shù)列A的所有“G時刻”組成的集合.
(1)對數(shù)列A:-2,2,-1,1,3,寫出![]() 的所有元素;
的所有元素;
(2)證明:若數(shù)列A中存在![]() 使得
使得![]() >
>![]() ,則
,則![]() ;
;
(3)證明:若數(shù)列A滿足![]() -
-![]() ≤1(n=2,3, …,N),則
≤1(n=2,3, …,N),則![]() 的元素個數(shù)不小于
的元素個數(shù)不小于![]() -
-![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系xOy中,曲線C的參數(shù)方程為![]() (α為參數(shù)),將C上每一點(diǎn)的橫坐標(biāo)保持不變,縱坐標(biāo)變?yōu)樵瓉淼?/span>3倍,得曲線C1.以O為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系.
(α為參數(shù)),將C上每一點(diǎn)的橫坐標(biāo)保持不變,縱坐標(biāo)變?yōu)樵瓉淼?/span>3倍,得曲線C1.以O為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系.
(1)求C1的極坐標(biāo)方程
(2)設(shè)M,N為C1上兩點(diǎn),若OM⊥ON,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com