
【題目】已知函數![]() .
.
(1)求函數![]() 的最大值;
的最大值;
(2)若函數![]() 與
與![]() 有相同極值點.
有相同極值點.
①求實數![]() 的值;
的值;
②若對于![]() (
(![]() 為自然對數的底數),不等式
為自然對數的底數),不等式![]() 恒成立,
恒成立,
求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)![]() ;(Ⅱ)(ⅰ)1; (ⅱ)
;(Ⅱ)(ⅰ)1; (ⅱ)![]() .
.
【解析】
試題(1)求導函數,確定函數的單調性,從而得函數![]() 的最大值;(2)(ⅰ)求導函數,利用函數
的最大值;(2)(ⅰ)求導函數,利用函數![]() 與
與![]() 有相同極值點,可得
有相同極值點,可得![]() 是函數
是函數![]() 的極值點,從而求解
的極值點,從而求解![]() 的值;(ⅱ)先求出
的值;(ⅱ)先求出![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,再將對于
,再將對于![]() ,不等式
,不等式![]() 恒成立,等價變形,分類討論,即可求解實數
恒成立,等價變形,分類討論,即可求解實數![]() 的取值范圍.
的取值范圍.
試題解析:(1)![]() ,
,
由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
∴![]() 在
在![]() 上為增函數,在
上為增函數,在![]() 上為減函數,
上為減函數,
∴函數![]() 的最大值為
的最大值為![]() ;
;
(2)∵![]() ,∴
,∴![]() ,
,
(Ⅰ)由(1)知,![]() 是函數
是函數![]() 的極值點,又∵函數
的極值點,又∵函數![]() 與
與![]() 有相同極值點,
有相同極值點,
∴![]() 是函數
是函數![]() 的極值點,∴
的極值點,∴![]() ,解得
,解得![]() ,
,
經檢驗,當![]() 時,函數
時,函數![]() 取到極小值,符合題意;
取到極小值,符合題意;
(ⅱ)∵![]() ,
,![]() ,
,![]() , ∵
, ∵![]() , 即
, 即![]() ,∴
,∴![]() ,
,![]() ,
,
由(ⅰ)知![]() ,∴
,∴![]() ,當
,當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
故![]() 在
在![]() 為減函數,在
為減函數,在![]() 上為增函數,∵
上為增函數,∵![]() ,
,
而![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,
,
①當![]() ,即
,即![]() 時,對于
時,對于![]() ,不等式
,不等式![]() 恒成立
恒成立
![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,又∵
,又∵![]() ,∴
,∴![]() ,
,
②當![]() ,即
,即![]() 時,對于
時,對于![]() ,不等式
,不等式![]() ,
,
![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,又∵
,又∵![]() ,
,
∴![]() .綜上,所求的實數
.綜上,所求的實數![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】小王參加一次比賽,比賽共設三關,第一、二關各有兩個必答題,如果每關兩個問題都答對,可進入下一關,第三關有三個問題,只要答對其中兩個問題,則闖關成功,每過一關可一次性獲得價值分別為1000元,3000元,6000元的獎品(不重復得獎),小王對三關中每個問題回答正確的概率依次為![]() ,
,![]() ,
,![]() ,且每個問題回答正確與否相互獨立.
,且每個問題回答正確與否相互獨立.
(1)求小王過第一關但未過第二關的概率;
(2)用![]() 表示小王所獲得獲品的價值,寫出
表示小王所獲得獲品的價值,寫出![]() 的概率分布列,并求
的概率分布列,并求![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為 為參數
為參數![]() ,以坐標原點O為極點,以x軸正半軸為極軸的極坐標系中,曲線C的極坐標方程為
,以坐標原點O為極點,以x軸正半軸為極軸的極坐標系中,曲線C的極坐標方程為![]() .
.
![]() 求直線l的普通方程及曲線C的直角坐標方程;
求直線l的普通方程及曲線C的直角坐標方程;
![]() 若直線l與曲線C交于A,B兩點,求線段AB的中點P到坐標原點O的距離.
若直線l與曲線C交于A,B兩點,求線段AB的中點P到坐標原點O的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年4月,北京世界園藝博覽會開幕,為了保障園藝博覽會安全順利地進行,某部門將5個安保小組全部安排到指定的三個不同區域內值勤,則每個區域至少有一個安保小組的排法有( )
A.150種B.240種C.300種D.360種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為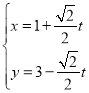 (
(![]() 為參數且
為參數且![]() ).在以坐標原點為極點,
).在以坐標原點為極點,![]() 軸的正半軸為極軸的極坐標系中,曲線
軸的正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的極坐標方程及曲線
的極坐標方程及曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() 在直線
在直線![]() 上,點
上,點![]() 在曲線
在曲線![]() 上,求證:
上,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國“一帶一路”戰略構思提出后,某科技企業為抓住“一帶一路”帶來的機遇,決定開發生產一款大型電子設備.生產這種設備的年固定成本為500萬元,每生產x臺,需另投入成本![]() 萬元
萬元![]() ,當年產量不足60臺時,
,當年產量不足60臺時,![]() 萬元
萬元![]() ;當年產量不小于60臺時,
;當年產量不小于60臺時,![]() 萬元
萬元![]() 若每臺設備售價為100萬元,通過市場分析,該企業生產的電子設備能全部售完.
若每臺設備售價為100萬元,通過市場分析,該企業生產的電子設備能全部售完.
![]() 求年利潤
求年利潤![]() 萬元
萬元![]() 關于年產量
關于年產量![]() 臺
臺![]() 的函數關系式;
的函數關系式;
![]() 當年產量為多少臺時,該企業在這一電子設備的生產中所獲利潤最大?
當年產量為多少臺時,該企業在這一電子設備的生產中所獲利潤最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com