已知 a>0,解關于x的不等式(x-3)[(a-1)x+3]>0.
【答案】
分析:分三種情況考慮:當a-1=0,即a=1時;當a-1小于0,即a大于0小于1時;當a-1大于0,即a大于1時,分別求出各種情況的解集即可.
解答:解:當a=1時,不等式變形為3(x-3)>0,解得:x>3;
當0<a<1時,變形為(x-3)[(1-a)x-3]<0,
可化為
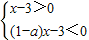
或
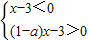
,
解得:3<x<
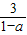
;
當a>1時,變形為
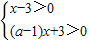
或
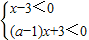
,
解得:x<
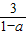
或x>3,
綜上,當a=1時,不等式的解集為{x|x>3};
當0<a<1時,不等式的解集為{x|3<x<
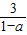
};
當a>1時,不等式的解集為{x|x|x<
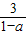
或x>3}.
點評:此題考查了一元二次不等式的解法,利用了分類討論的思想,分類討論時要做到不重不漏,考慮問題要全面.

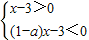 或
或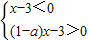 ,
,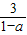 ;
;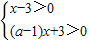 或
或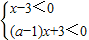 ,
,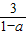 或x>3,
或x>3,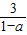 };
};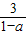 或x>3}.
或x>3}.
