
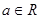 ,函數(shù)
,函數(shù)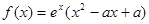 .
.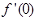 的值;
的值;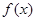 的單調(diào)區(qū)間.
的單調(diào)區(qū)間.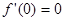 ;(Ⅱ)詳見解析.
;(Ⅱ)詳見解析.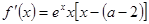 ,然后代入
,然后代入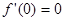 ;
;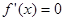 ,得
,得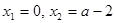 ,然后分析二根之間的關(guān)系,需要分類討論,按
,然后分析二根之間的關(guān)系,需要分類討論,按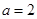 ;
;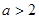 ;
;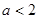 進(jìn)行.
進(jìn)行.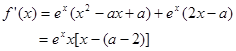
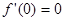 . 3分
. 3分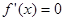 ,得
,得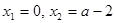 4分
4分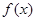 定義域?yàn)镽,且對任意
定義域?yàn)镽,且對任意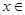 R,
R,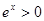 ,
,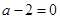 ,即
,即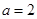 時,
時,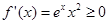 ,
,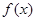 的單調(diào)遞增區(qū)間是
的單調(diào)遞增區(qū)間是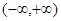 . 6分
. 6分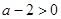 ,即
,即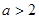 時,
時,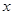 | 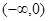 | 0 | 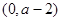 | 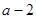 | 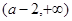 |
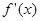 | + | 0 | - | 0 | + |
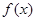 | ↗ | | ↘ | | ↗ |
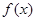 的單調(diào)遞增區(qū)間是
的單調(diào)遞增區(qū)間是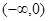 ,
,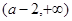 ,單調(diào)遞減區(qū)間是
,單調(diào)遞減區(qū)間是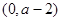 . 9分
. 9分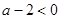 ,即
,即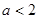 時,
時,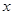 | 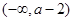 | 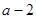 | 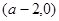 | 0 | 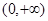 |
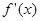 | + | 0 | - | 0 | + |
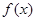 | ↗ | | ↘ | | ↗ |
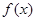 的單調(diào)遞增區(qū)間是
的單調(diào)遞增區(qū)間是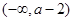 ,
,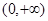 ,單調(diào)遞減區(qū)間是
,單調(diào)遞減區(qū)間是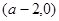 . 12分
. 12分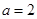 時,
時,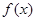 的單調(diào)遞增區(qū)間是
的單調(diào)遞增區(qū)間是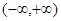 .
. 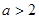 時,
時,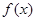 的單調(diào)遞增區(qū)間是
的單調(diào)遞增區(qū)間是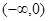 ,
,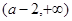 ,
,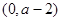 .
.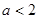 時,
時,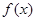 的單調(diào)遞增區(qū)間是
的單調(diào)遞增區(qū)間是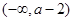 ,
,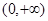 ,
,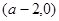 . 13分
. 13分


| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
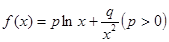 ,若
,若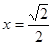 時,
時,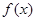 有極小值
有極小值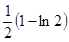 ,
,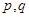 的取值;
的取值;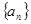 中,
中,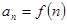 ,求證:數(shù)列
,求證:數(shù)列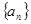 的前
的前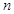 項(xiàng)和
項(xiàng)和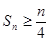 ;
;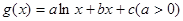 ,若
,若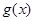 有極值且極值為
有極值且極值為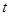 ,則
,則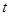 與
與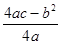 是否具有確定的大小關(guān)系?證明你的結(jié)論.
是否具有確定的大小關(guān)系?證明你的結(jié)論.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
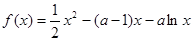 ,
,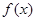 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;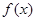 在區(qū)間
在區(qū)間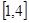 內(nèi)的最小值為
內(nèi)的最小值為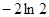 ,求
,求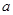 的值.(參考數(shù)據(jù)
的值.(參考數(shù)據(jù)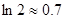 )
)查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
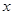 元/本(9≤
元/本(9≤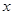 ≤11),預(yù)計(jì)一年的銷售量為
≤11),預(yù)計(jì)一年的銷售量為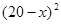 萬本.
萬本.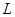 (萬元)與每本書的定價
(萬元)與每本書的定價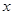 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;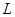 最大,并求出
最大,并求出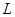 的最大值
的最大值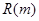 .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
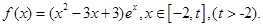
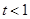 時,求函數(shù)
時,求函數(shù)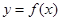 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;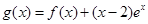 ,試問函數(shù)
,試問函數(shù)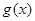 在
在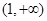 上是否存在保值區(qū)間?若存在,請求出一個保值區(qū)間;若不存在,請說明理由.
上是否存在保值區(qū)間?若存在,請求出一個保值區(qū)間;若不存在,請說明理由.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
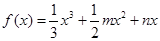 ,
,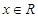 .
.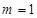 ,
,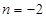 時,求
時,求 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;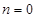 ,且
,且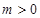 時,求
時,求 在區(qū)間
在區(qū)間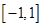 上的最大值.
上的最大值.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
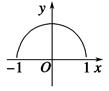
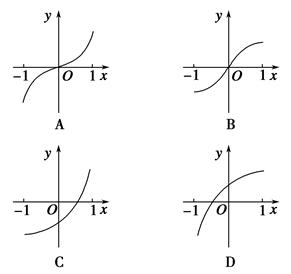
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
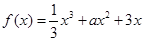 在(0, 1)上不是單調(diào)函數(shù),則實(shí)數(shù)
在(0, 1)上不是單調(diào)函數(shù),則實(shí)數(shù)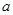 的取值范圍為 _____.
的取值范圍為 _____.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com