【題目】已知直線2x+y﹣k=0（k＞0）與圓x2+y2=4交于不同的兩點A，B，O是坐標原點，且有| 
| 
| 
|，那么k的取值范圍是（ ）
A.[ 
，+∞）
B.[ ，2 ）
C.[ 
，+∞）
D.[ ，2 ）
輕松奪冠全能掌控卷系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）=﹣f'（0）ex+2x，點P為曲線y=f（x）在點（0，f（0））處的切線l上的一點，點Q在曲線y=ex上，則|PQ|的最小值為 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=x2+ax﹣lnx，a∈R．
（1）若函數f（x）在[1，2]上是減函數，求實數a的取值范圍；
（2）令g（x）=f（x）﹣x2 ， 是否存在實數a，當x∈（0，e]（e是自然常數）時，函數g（x）的最小值是3，若存在，求出a的值；若不存在，說明理由；
（3）求證：當x∈（0，e]時，e2x2﹣ 
x＞（x+1）lnx．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數 
．
（1）求函數y=f（x）的最小正周期；
（2）已知△ABC中，角A，B，C的對邊分別是a，b，c，且a，b，c成等比數列，求f（B）的范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，已知以M為圓心的圓M：x2+y2﹣12x﹣14y+60=0及其上的一點A（2，4）．
（Ⅰ）是否存在直線l：y=kx+3與圓M有兩個交點B，C，并且|AB|=|AC|，若有，求此直線方程，若沒有，請說明理由；
（Ⅱ）設點T（t，0）滿足：存在圓M上的兩點P和Q，使得 
= 
，求實數t的取值范圍．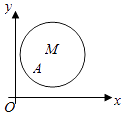
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若三棱錐P﹣ABC中，AB=AC=1，AB⊥AC，PA⊥平面ABC，且直線PA與平面PBC所成角的正切值為 
，則三棱錐P﹣ABC的外接球的表面積為（ ）
A.4π
B.8π
C.16π
D.32π
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
