已知直線l:(a-2)y=(3a-1)x-1①求證:無論a為何值時,直線總過第一象限;②為使這條直線不過第二象限,求a的取值范圍;③若直線l交x軸負半軸于A,交y軸正半軸于B.△AOB的面積為S且-2≤a≤-1,求S的最小值并求此時直線l的方程.
【答案】
分析:①由于(3x-y)+(-x+2y-1)=0對任意實數a恒過直線3x-y=0與x-2y+1=0的交點即可得出結論;
②先對a進行分類討論:當a=2時,直線為
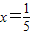
,不過第二象限;當a≠2時,a≥2時直線不過第二象限.從而得到結果;
③令x=0和令y=0得到直線在坐標軸上截距,再利用三角形面積公式得到S關于a的函數表達式,最后利用函數的單調性求得其最小值并求此時直線l的方程.
解答:解:①∵(3x-y)+(-x+2y-1)=0對任意實數a恒過直線3x-y=0與x-2y+1=0的交點
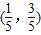
.
∴直線系恒過第一象限內的定點
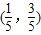
.
②當a=2時,直線為
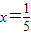
,不過第二象限;當a≠2時,直線方程化為
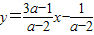
不過第二象限的充要條件為
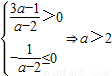
∴a≥2時直線不過第二象限.
③令x=0得
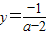
令y=0得
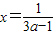
∴
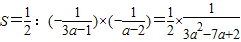
∵S在a∈[-2,-1]↗∴當a=-2時
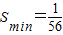
此時l:7x-4y+1=0
點評:本小題主要考查直線的方程、確定直線位置的幾何要素、恒過定點的直線等基礎知識,考查運算求解能力,考查數形結合思想、化歸與轉化思想.屬于基礎題.

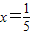 ,不過第二象限;當a≠2時,a≥2時直線不過第二象限.從而得到結果;
,不過第二象限;當a≠2時,a≥2時直線不過第二象限.從而得到結果;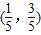 .
.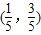 .
.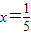 ,不過第二象限;當a≠2時,直線方程化為
,不過第二象限;當a≠2時,直線方程化為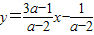
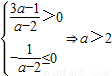
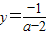
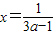 ∴
∴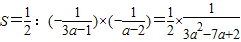
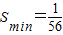


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案