
已函數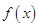 是定義在
是定義在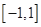 上的奇函數,在
上的奇函數,在 上時
上時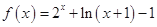
(Ⅰ)求函數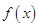 的解析式;
的解析式;
(Ⅱ)解不等式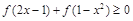 .
.
(Ⅰ) ;(Ⅱ)[0,1]
;(Ⅱ)[0,1]
【解析】
試題分析:(Ⅰ)由奇函數及在[0,1]上的解析式可得函數在[-1,0]上的解析式.從而即可得在[-1,1]上的解析式.本小題主要是考查分段函數的解析式問題.
(Ⅱ)由題意可知函數f(x)在[-1,1]上是遞增函數.又因為函數f(x)是奇函數.所以通過 可得.
可得. 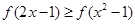 所以可得
所以可得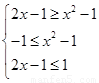 .從而可解得結論.本小題關鍵是通過函數的單調遞增把函數值的大小轉化為自變量的大小比較.
.從而可解得結論.本小題關鍵是通過函數的單調遞增把函數值的大小轉化為自變量的大小比較.
試題解析:(Ⅰ)設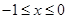 .則
.則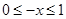 .所以
.所以 .又f(x)是奇函數.所以f(-x)=-f(x).f(x)=-f(-x)=
.又f(x)是奇函數.所以f(-x)=-f(x).f(x)=-f(-x)=
 .所以
.所以 .
.
(Ⅱ)易知f(x)是[-1,1]上增函數.由已知得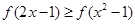 .等價于
.等價于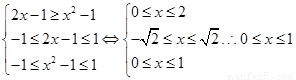 .所以不等式的解集為[0,1].
.所以不等式的解集為[0,1].
考點:1.分段函數.2.函數的單調性.3.函數的奇偶性.


 期末100分闖關海淀考王系列答案
期末100分闖關海淀考王系列答案 小學能力測試卷系列答案
小學能力測試卷系列答案科目:高中數學 來源:2014屆湖北孝感高中高三年級九月調研考試理科數學試卷(解析版) 題型:解答題
已函數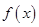 是定義在
是定義在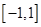 上的奇函數,在
上的奇函數,在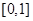 上
上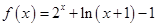 .
.
(1)求函數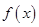 的解析式;并判斷
的解析式;并判斷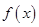 在
在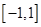 上的單調性(不要求證明);
上的單調性(不要求證明);
(2)解不等式 .
.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年貴州省第13次月考) 題型:解答題
已知函數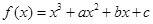 是定義在
是定義在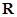 上的奇函數,其圖象過點
上的奇函數,其圖象過點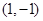 和
和
點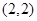 .
.
(Ⅰ)求函數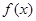 的解析式,并求
的解析式,并求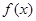 的單調區間;
的單調區間;
(Ⅱ)設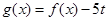 ,當實數
,當實數 如何取值時,關于
如何取值時,關于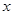 的方程
的方程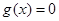 有且只有一個實
有且只有一個實
數根?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com