若曲線C:y=ax+lnx存在斜率為1的切線,則實數a的取值范圍是 .
【答案】
分析:先求出函數的定義域,然后求出導函數,根據存在斜率為1的切線,得到此時斜率為1,問題轉化為x>0范圍內導函數

存在實數解,再將之轉化為

進行實數a的取值范圍即可.
解答:解:由題意該函數的定義域x>0,由

.
因為存在斜率為1的切線,
故此時斜率為1,問題轉化為x>0范圍內導函數

存在實數解.
再將之轉化為
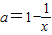
∵x>0,
∴a<1
故答案為:{a|a<1}.
點評:本題主要考查了利用導數研究曲線上某點切線方程,方程有解等有關基礎知識,考查運算求解能力、推理論證能力與轉化思想,屬于基礎題.

 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案