雙曲線x2-16y2=16左右焦點分別為F1,F2,直線l過雙曲線的左焦點F1交雙曲線的左支與A,B,且|AB|=12,則△ABF2的周長為 .
【答案】
分析:由雙曲線x
2-16y
2=16左右焦點分別為F
1,F
2,直線l過雙曲線的左焦點F
1交雙曲線的左支與A,B,且|AB|=12,知|AF
2|+|BF
2|-|AB|=4a=16,由此能求出△ABF
2的周長.
解答:解:∵x
2-16y
2=16,∴
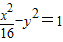
,
∵雙曲線x
2-16y
2=16左右焦點分別為F
1,F
2,
直線l過雙曲線的左焦點F
1交雙曲線的左支與A,B,且|AB|=12,
∴|AF
2|+|BF
2|-|AB|=4a=16,
∴AF
2|+|BF
2|=28,
∴△ABF
2的周長=|AF
2|+|BF
2|+|AB|=40.
故答案為:40.
點評:本題考查三角形的周長的求法,具體涉及到雙曲線的簡單性質,直線與雙曲線的位置的綜合運用,解題時要認真審題,注意等價轉化思想的合理運用.

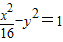 ,
,
