分析:(1)λ=1時,
=,以C為原點,CB為x軸,DC為y軸,CC
1為z軸,建立空間直角坐標系,則
=(0,2,2),
=(-1,0,2),設平面FDE的法向量為
,則
=(0,0,1),設平面FDE的法向量為
=(x,y,z),由
•=0,•=0,得
=(2,-1,1),由向量法能求出二面角F-DE-C的余弦值.
(2)由D
1(0,-2,4),B(2,0,0),E(1,0,0)設F(0,0,t),則
=(-2,-2,4),
=(-1,0,t),要使EF⊥BD
1,只要
•=0,由此能求出λ.
解答:解:(1)λ=1時,
=,
以C為原點,CB為x軸,DC為y軸,CC
1為z軸,建立空間直角坐標系,
∵正四棱柱ABCD-A
1B
1C
1D
1中,AB=2,AA
1=4,E為BC的中點,
∴E(1,0,0),F(0,0,2),D(0,-2,0),F(0,0,2),
∴
=(0,2,2),
=(-1,0,2),
設平面FDE的法向量為
,則
=(0,0,1),
設平面FDE的法向量為
=(x,y,z),則
•=0,•=0,
∴
,
∴
=(2,-1,1),
∴
cos<,>= =
,
∴二面角F-DE-C的余弦值為
.
(2)∵D
1(0,-2,4),B(2,0,0),E(1,0,0)
設F(0,0,t),則
=(-2,-2,4),
=(-1,0,t),
∵EF⊥BD
1,
∴
•=0,
∴2+4t=0,
解得t=-
.
∴F(0,0,-
)
∴
=(0,0,-),
=(0,0,),
∴λ=
=-9.
點評:本題考查二面角的余弦值的求法和求λ為何值時,有BD1⊥EF.解題時要認真審題,仔細解答,注意合理地把空間問題轉化為平面問題,注意向量法的靈活運用.

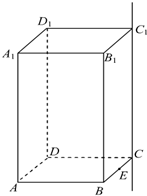 如圖,已知正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4,E為BC的中點,F為直線CC1上的動點,設
如圖,已知正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4,E為BC的中點,F為直線CC1上的動點,設

 如圖,已知正四棱柱ABCD-A1B1C1D1,點E在棱D1D上,截面EAC∥D1B,且面EAC與底面ABCD所成的角為45°,AB=a.
如圖,已知正四棱柱ABCD-A1B1C1D1,點E在棱D1D上,截面EAC∥D1B,且面EAC與底面ABCD所成的角為45°,AB=a. 如圖,已知正四棱柱ABCD-A1B1C1D1 的底面邊長為3,側棱長為4,連接A1B,過A作AF⊥A1B垂足為F,且AF的延長線交B1B于E.
如圖,已知正四棱柱ABCD-A1B1C1D1 的底面邊長為3,側棱長為4,連接A1B,過A作AF⊥A1B垂足為F,且AF的延長線交B1B于E.
 如圖,已知正四棱柱ABCD-A1B1C1D1,點E在棱D1D上,截面EAC∥D1B,且面EAC與底面ABCD所成的角為45°,AB=a.
如圖,已知正四棱柱ABCD-A1B1C1D1,點E在棱D1D上,截面EAC∥D1B,且面EAC與底面ABCD所成的角為45°,AB=a.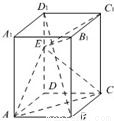 如圖,已知正四棱柱ABCD-A1B1C1D1,點E在棱D1D上,截面EAC∥D1B,且面EAC與底面ABCD所成的角為45°,AB=a.
如圖,已知正四棱柱ABCD-A1B1C1D1,點E在棱D1D上,截面EAC∥D1B,且面EAC與底面ABCD所成的角為45°,AB=a.