
【題目】楊輝三角,是二項式系數在三角形中的一種幾何排列.中國南宋數學家楊輝1261年所著的《詳解九章算法》一書中出現了楊輝三角.在歐洲,帕斯卡在1654年也發現了這一規律,所以這個表又叫做帕斯卡三角形.楊輝三角是中國古代數學的杰出研究成果之一,它把二項式系數圖形化,把組合數內在的一些代數性質直觀地從圖形中體現出來,是一種離散型的數與形的結合.
第0行 | 1 |
第1行 | 1 1 |
第2行 | 1 2 1 |
第3行 | 1 3 3 1 |
第4行 | 1 4 6 4 1 |
第5行 | 1 5 10 10 5 1 |
第6行 | 1 6 15 20 15 6 1 |
(1)記楊輝三角的前n行所有數之和為![]() ,求
,求![]() 的通項公式;
的通項公式;
(2)在楊輝三角中是否存在某一行,且該行中三個相鄰的數之比為![]() ?若存在,試求出是第幾行;若不存在,請說明理由;
?若存在,試求出是第幾行;若不存在,請說明理由;
(3)已知n,r為正整數,且![]() .求證:任何四個相鄰的組合數
.求證:任何四個相鄰的組合數![]() ,
,![]() ,
,![]() ,
,![]() 不能構成等差數列.
不能構成等差數列.
【答案】(1)![]() (2)存在;第62行(3)證明見解析
(2)存在;第62行(3)證明見解析
【解析】
(1)由二項式定理的性質,楊輝三角第![]() 行的n個數的和為:
行的n個數的和為:![]() ,然后求出
,然后求出![]() 即可
即可
(2)由方程![]() ,
,![]() 解出即可
解出即可
(3)若有n,r(![]() ),使得
),使得![]() ,
,![]() ,
,![]() ,
,![]() 成等差數列,則由等差中項和組合數的知識可得出
成等差數列,則由等差中項和組合數的知識可得出![]() ,然后可得
,然后可得![]() ,這與
,這與![]() ,
,![]() ,
,![]() ,
,![]() 成等差數列相矛盾.
成等差數列相矛盾.
(1)由二項式定理的性質,楊輝三角第![]() 行的n個數的和為:
行的n個數的和為:
![]() ,
,
∴![]() .
.
(2)楊輝三角形的第n行由二項式系數![]() ,
,![]() ,1,2,…,n組成.
,1,2,…,n組成.
如果第n行中有![]() ,
,![]() ,
,
那么![]() ,
,![]() ,
,
解這個聯立方程組,得![]() ,
,![]() .
.
即第62行有三個相鄰的數![]() ,
,![]() ,
,![]() 的比為
的比為![]() .
.
(3)若有n,r(![]() ),使得
),使得![]() ,
,![]() ,
,![]() ,
,![]() 成等差數列,
成等差數列,
則![]() ,
,![]() ,
,
即![]() ,
,
![]() .
.
所以有![]() ,
,
![]() ,
,
經整理得到![]() ,
,![]() .
.
兩式相減可得![]()
而由二項式系數的性質可知![]() ,
,
這與![]() ,
,![]() ,
,![]() ,
,![]() 成等差數列矛盾,
成等差數列矛盾,
所以原命題得證.


科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為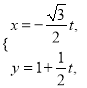 (
(![]() 為參數),以原點為極點,
為參數),以原點為極點, ![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的方程為
的方程為![]() ,定點
,定點![]() ,點
,點![]() 是曲線
是曲線![]() 上的動點,
上的動點, ![]() 為
為![]() 的中點.
的中點.
(1)求點![]() 的軌跡
的軌跡![]() 的直角坐標方程;
的直角坐標方程;
(2)已知直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,與曲線
,與曲線![]() 的交點為
的交點為![]() ,若
,若![]() 的中點為
的中點為![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知長度為![]() 的線段
的線段![]() 的兩個端點
的兩個端點![]() 分別在
分別在![]() 軸和
軸和![]() 軸上運動,動點
軸上運動,動點![]() 滿足
滿足![]() ,設動點
,設動點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)過點![]() ,且斜率不為零的直線
,且斜率不為零的直線![]() 與曲線
與曲線![]() 交于兩點
交于兩點![]() ,在
,在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得直線
,使得直線![]() 與
與![]() 的斜率之積為常數?若存在,求出定點
的斜率之積為常數?若存在,求出定點![]() 的坐標以及此常數;若不存在,請說明理由.
的坐標以及此常數;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學生想在物理、化學、生物、政治、歷史、地理、技術這七門課程中選三門作為選考科目,下列說法錯誤的是( )
A.若任意選擇三門課程,選法總數為![]()
B.若物理和化學至少選一門,選法總數為![]()
C.若物理和歷史不能同時選,選法總數為![]()
D.若物理和化學至少選一門,且物理和歷史不能同時選,選法總數為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,且橢圓上存在一點
,且橢圓上存在一點![]() ,滿足
,滿足![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過橢圓![]() 右焦點
右焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,求
,求![]() 的內切圓的半徑的最大值.
的內切圓的半徑的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線E:![]() -
-![]() =1(a>0,b>0)的右頂點為A,O為坐標原點,M為OA的中點,若以AM為直徑的圓與E的漸近線相切,則雙曲線E的離心率等于( )
=1(a>0,b>0)的右頂點為A,O為坐標原點,M為OA的中點,若以AM為直徑的圓與E的漸近線相切,則雙曲線E的離心率等于( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com