
【題目】已知函數 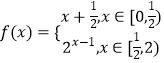 ,若存在x1 , x2 , 當0≤x1<x2<2時,f(x1)=f(x2),則x1f(x2)﹣f(x2)的取值范圍為( )
,若存在x1 , x2 , 當0≤x1<x2<2時,f(x1)=f(x2),則x1f(x2)﹣f(x2)的取值范圍為( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:作出函數的圖象:
∵存在x1 , x2 , 當0≤x1<x2<2時,f(x1)=f(x2)
∴0≤x1< ![]() ,
,
∵x+ ![]() 在[0,
在[0, ![]() )上的最小值為
)上的最小值為 ![]() ;
;
2x﹣1在[ ![]() ,2)的最小值為
,2)的最小值為 ![]() ,
,
∴x1+ ![]() ≥
≥ ![]() ,x1≥
,x1≥ ![]() ,
,
∴ ![]() ≤x1<
≤x1< ![]() .
.
∵f(x1)=x1+ ![]() ,f(x1)=f(x2)
,f(x1)=f(x2)
∴x1f(x2)﹣f(x2)=x1f(x1)﹣f(x1)2
= ![]() ﹣(x1+
﹣(x1+ ![]() )=x12﹣
)=x12﹣ ![]() x1﹣
x1﹣ ![]() ,
,
設y=x12﹣ ![]() x1﹣
x1﹣ ![]() =(x1﹣
=(x1﹣ ![]() )2﹣
)2﹣ ![]() ,(
,( ![]() ≤x1<
≤x1< ![]() ),
),
則對應拋物線的對稱軸為x= ![]() ,
,
∴當x= ![]() 時,y=﹣
時,y=﹣ ![]() ,
,
當x= ![]() 時,y=
時,y= ![]() ,
,
即x1f(x2)﹣f(x2)的取值范圍為[﹣ ![]() ,
, ![]() ).
).
故選:B.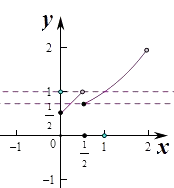


 名題金卷系列答案
名題金卷系列答案科目:高中數學 來源: 題型:
【題目】已知![]() ,設
,設![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() 為常數).
為常數).
(1)求![]() 的最小值及相應的
的最小值及相應的![]() 的值;
的值;
(2)設![]() ,若
,若![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)若對任意![]() ,以
,以![]() 、
、![]() 、
、![]() 為三邊長總能構成三角形,求
為三邊長總能構成三角形,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐S﹣ABCD,SB⊥AD,側面SAD是邊長為4的等邊三角形,底面ABCD為菱形,側面SAD與底面ABCD所成的二面角為120°.
(1)求點S到平面ABCD的距離;
(2)若E為SC的中點,求二面角A﹣DE﹣C的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某海關對同時從![]() 三個不同地區進口的某種商品進行隨機抽樣檢測,已知從
三個不同地區進口的某種商品進行隨機抽樣檢測,已知從![]() 三個地區抽取的商品件數分別是50,150,100.檢測人員再用分層抽樣的方法從海關抽樣的這些商品中隨機抽取6件樣品進行檢測.
三個地區抽取的商品件數分別是50,150,100.檢測人員再用分層抽樣的方法從海關抽樣的這些商品中隨機抽取6件樣品進行檢測.
(1)求這6件樣品中,來自![]() 各地區商品的數量;
各地區商品的數量;
(2)若在這6件樣品中隨機抽取2件送往另一機構進行進一步檢測,求這2件樣品來自相同地區的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在多面體![]() 中,
中, ![]() 與
與![]() 均為邊長為2的正方形,
均為邊長為2的正方形, ![]() 為等腰直角三角形,
為等腰直角三角形, ![]() ,且平面
,且平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某汽配廠生產某種零件,每個零件的出廠單價為60元,為了鼓勵更多銷售商訂購,該廠決定當一次訂購超過100個時,每多訂購一個,訂購的全部零件的出廠單價就降低![]() 元,但實際出廠單價不低于51元.
元,但實際出廠單價不低于51元.
![]() 當一次訂購量最少為多少時,零件的實際出廠單價恰好為51元?
當一次訂購量最少為多少時,零件的實際出廠單價恰好為51元?
![]() 設一次訂購量為x個,零件的實際出廠單價為p元,寫出函數
設一次訂購量為x個,零件的實際出廠單價為p元,寫出函數![]() 的表達式.
的表達式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以原點為極點,x軸的正半軸為極軸建立極坐標系,已知曲線C:ρsin2θ=2acosθ(a>0),直線l的參數方程為  (t為參數),l與C分別交于M,N,P(﹣2,﹣4).
(t為參數),l與C分別交于M,N,P(﹣2,﹣4).
(1)寫出C的平面直角坐標系方程和l的普通方程;
(2)已知|PM|,|MN|,|PN|成等比數列,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,我國許多省市霧霾天氣頻發,為增強市民的環境保護意識,某市面向全市征召n名義務宣傳志愿者,成立環境保護宣傳組織![]() 現把該組織的成員按年齡分成5組:第1組
現把該組織的成員按年齡分成5組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示,已知第2組有70人.
,得到的頻率分布直方圖如圖所示,已知第2組有70人.
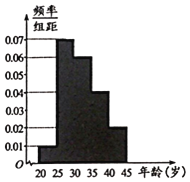
(1)求該組織的人數.
(2)若從第3,4,5組中用分層抽樣的方法抽取6名志愿者參加某社區的宣傳活動,然后在這6名志愿者中隨機抽取2名志愿者介紹宣傳經驗,求第3組至少有一名志愿者被抽中的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com