
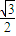 ,且f(0)=
,且f(0)=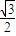 ,f(
,f(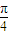 )=
)= .
.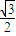 ,f(
,f(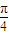 )=
)= 求得:a=
求得:a=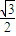 ,b=1,然后化簡(jiǎn)函數(shù)利用降次、“合二為一”后得f(x)=sin(2x+
,b=1,然后化簡(jiǎn)函數(shù)利用降次、“合二為一”后得f(x)=sin(2x+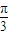 ),
),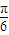 個(gè)單位后圖象關(guān)于原點(diǎn)對(duì)稱即為奇函數(shù).
個(gè)單位后圖象關(guān)于原點(diǎn)對(duì)稱即為奇函數(shù).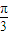 )=cos[2(x-
)=cos[2(x-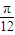 )],方案一:選向左平移,然后再伸縮變換.
)],方案一:選向左平移,然后再伸縮變換.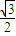 ,f(
,f(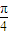 )=
)= 得:a=
得:a=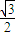 ,b=1,所以,函數(shù)f(x)=2acos2x+bsinxcosx-
,b=1,所以,函數(shù)f(x)=2acos2x+bsinxcosx-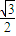 =sin(2x+
=sin(2x+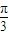 ),
),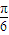 ,0)對(duì)稱,向右平移
,0)對(duì)稱,向右平移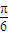 個(gè)單位后圖象關(guān)于原點(diǎn)對(duì)稱即為奇函數(shù)(平移的方法不唯一,因?yàn)楹瘮?shù)y=f(x)的圖象對(duì)稱中心不唯一);
個(gè)單位后圖象關(guān)于原點(diǎn)對(duì)稱即為奇函數(shù)(平移的方法不唯一,因?yàn)楹瘮?shù)y=f(x)的圖象對(duì)稱中心不唯一);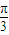 ),要使其為奇函數(shù),則x=0時(shí)函數(shù)值為0(奇函數(shù)圖象關(guān)于原點(diǎn)對(duì)稱),即-2m+
),要使其為奇函數(shù),則x=0時(shí)函數(shù)值為0(奇函數(shù)圖象關(guān)于原點(diǎn)對(duì)稱),即-2m+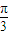 =kπ,k∈Z⇒m=-
=kπ,k∈Z⇒m=-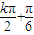 ,k∈Z,隨k的取值不同可以得到不同的m的值,回答其中任一個(gè)即可.(運(yùn)算量雖大一些,但更具一般性).
,k∈Z,隨k的取值不同可以得到不同的m的值,回答其中任一個(gè)即可.(運(yùn)算量雖大一些,但更具一般性).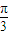 )=cos(
)=cos(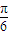 -2x)=cos(2x-
-2x)=cos(2x-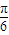 )=cos[2(x-
)=cos[2(x-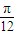 )],方案一:先左移
)],方案一:先左移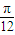 (x變成x+
(x變成x+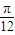 )得到函數(shù)y=cos2x,再縱坐標(biāo)不變橫坐標(biāo)變?yōu)樵瓉淼?倍(x變成
)得到函數(shù)y=cos2x,再縱坐標(biāo)不變橫坐標(biāo)變?yōu)樵瓉淼?倍(x變成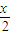 )得到函數(shù)y=cosx;
)得到函數(shù)y=cosx;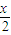 )得到函數(shù)y=cos(x-
)得到函數(shù)y=cos(x-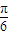 ),再左移
),再左移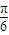 (x變成x+
(x變成x+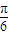 )得到函數(shù)y=cosx.
)得到函數(shù)y=cosx.

 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
| 1 |
| x |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com