
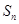 為數列
為數列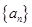 的前
的前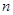 項和,對任意的
項和,對任意的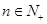 ,都有
,都有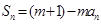 (
(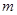 為正常數).
為正常數).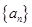 是等比數列;
是等比數列;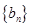 滿足
滿足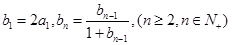 求數列
求數列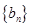 的通項公式;
的通項公式;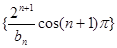 的前
的前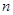 項和
項和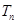 .
.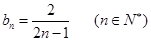 ;(3)
;(3) .
. 求出
求出 與
與 的關系,判斷數列是等差數列,從而寫出等差數列的通項公式;(2)因為
的關系,判斷數列是等差數列,從而寫出等差數列的通項公式;(2)因為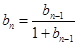 ,所以可以證明
,所以可以證明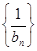 是首項為
是首項為 ,公差為1的等差數列,先求出
,公差為1的等差數列,先求出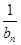 的通項公式,再求
的通項公式,再求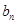 ;(3)把第(2)問的
;(3)把第(2)問的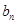 代入,利用錯位相減法求
代入,利用錯位相減法求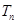 .
. 時,
時, ,解得
,解得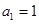 . 1分
. 1分 時,
時,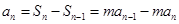 .即
.即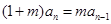 . 2分
. 2分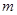 為常數,且
為常數,且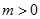 ,∴
,∴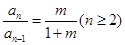 .
. 是首項為1,公比為
是首項為1,公比為 的等比數列. 3分
的等比數列. 3分 . 4分
. 4分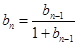 ,∴
,∴
 ,即
,即 . 5分
. 5分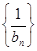 是首項為
是首項為 ,公差為1的等差數列. 6分
,公差為1的等差數列. 6分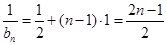 ,即
,即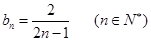 . 7分
. 7分 ,則
,則
 8分
8分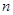 為偶數時,
為偶數時,
 ①
① ②
②

 =
=
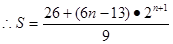 10分
10分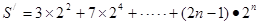 ③
③ ④
④
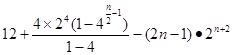
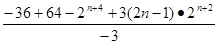 =
=
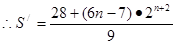 11分
11分
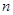 為奇數時,
為奇數時,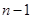 為偶數,
為偶數, 

 14分
14分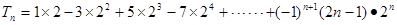 ①
①  ②
② 10分
10分  12分
12分 
 13分
13分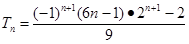 14分
14分

 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com