【答案】
分析:函數y=|x-1|+|x-2|+…+|x-2012|表示數軸上的x對應點到1,2,3,4…2012的距離之和,f(x)的圖象關于直線 x=
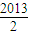
對稱如圖所示:結合圖形得出結論.
解答:解:由絕對值的意義可得函數y=|x-1|+|x-2|+…+|x-2012|表示數軸上的x對應點到1,2,3,4…2012的距離之和,
當x∈[1,2012]時,|x-1|+|x-2012|取得最小值等于2011,
當x∈[2,2011]時,|x-2|+|x-2011|取得最小值等于2009,
當x∈[3,2010]時,|x-3|+|x-2010|取得最小值等于2007,
…
當x∈[1006,1007]時,|x-1006|+|x-1007|取得最小值等于1.
故當x∈[1006,1007]時,函數y=|x-1|+|x-2|+…+|x-2012|=(|x-1|+|x-2012|)+(|x-2|+|x-2011|)+(|x-3|+|x-2010|)+…(|x-1006|+|x-1007|)
取得最小值為2011+2009+2007+…+1=1006
2.
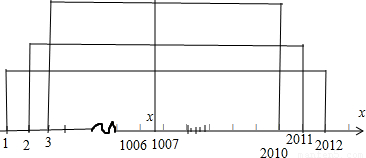
故函數 f(x)的圖象關于直線 x=
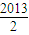
對稱.
當x<1時,函數y=(1-x)+(2-x)+(3-x)+…+(2012-x)=-2012x+2013×1006,
當x>2012時,函數y=(x-1)+(x-2)+(x-3)+…+(x-2012)=2012x-2013×1006,
如圖所示:
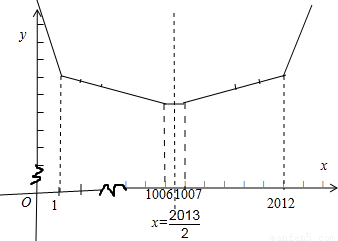
故圖象有對稱軸,且在對稱軸右側單調遞增,
故選D.
點評:本題主要考查絕對值的意義,帶有絕對值的函數,體現了數形結合、分類討論的數學思想,屬于中檔題.

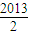 對稱如圖所示:結合圖形得出結論.
對稱如圖所示:結合圖形得出結論.
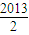 對稱.
對稱.

