
【題目】設直線![]() 與直線
與直線![]() 分別與橢圓
分別與橢圓![]()
![]() 交于點
交于點![]() ,且四邊形
,且四邊形![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設過點![]() 的動直線
的動直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,是否存在經過原點,且以
兩點,是否存在經過原點,且以![]() 為直徑的圓?若有,請求出圓的方程,若沒有,請說明理由.
為直徑的圓?若有,請求出圓的方程,若沒有,請說明理由.
【答案】(1)![]() ;(2)存在,圓的方程為
;(2)存在,圓的方程為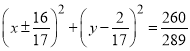 .
.
【解析】
(1)根據兩條直線解析式特征可知直線![]() 與直線
與直線![]() 關于坐標軸對稱,則
關于坐標軸對稱,則![]() 為矩形,將
為矩形,將![]() 與橢圓方程聯立,表示出交點的橫縱坐標,即可由四邊形
與橢圓方程聯立,表示出交點的橫縱坐標,即可由四邊形![]() 的面積確定參數,求得橢圓
的面積確定參數,求得橢圓![]() 的方程;
的方程;
(2)設直線![]() 的方程
的方程![]() ,兩個交點坐標
,兩個交點坐標![]() .聯立橢圓方程后化簡,用韋達定理表示出
.聯立橢圓方程后化簡,用韋達定理表示出![]() ,經過原點,且以
,經過原點,且以![]() 為直徑的圓滿足
為直徑的圓滿足![]() ,即
,即![]() ,由平面向量數量積的坐標運算代入即可求得斜率
,由平面向量數量積的坐標運算代入即可求得斜率![]() .由中點坐標公式即可求得線段
.由中點坐標公式即可求得線段![]() 中點
中點![]() 的坐標,進而求得
的坐標,進而求得![]() 的值,即可得圓的標準方程.
的值,即可得圓的標準方程.
(1)由題意可知直線![]() 與直線
與直線![]() 關于坐標軸對稱,所以四邊形
關于坐標軸對稱,所以四邊形![]() 為矩形,
為矩形,
則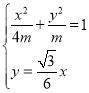 ,解得
,解得![]()
所以![]() ,
,
解得![]() ,
,
代入橢圓方程可得![]() .
.
(2)存在.
設![]() ,由題意可知直線
,由題意可知直線![]() 的斜率必然存在.
的斜率必然存在.
直線![]() 過點
過點![]() ,設直線
,設直線![]() 的方程為
的方程為![]() ,
,
則 ,化簡可得
,化簡可得![]() ,
,
所以![]() ,
,
經過原點,且以![]() 為直徑的圓滿足
為直徑的圓滿足![]() ,即
,即![]() ,
,
則![]()
![]()
![]()
![]()
![]() ,
,
解方程可得![]() ,經檢驗可知都滿足
,經檢驗可知都滿足![]() .
.
設線段![]() 的中點為
的中點為![]() .
.
則![]()
![]()
所以![]() ,
,
所以存在滿足條件的圓,圓的方程為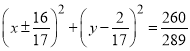 .
.


 課前課后同步練習系列答案
課前課后同步練習系列答案 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案 一卷搞定系列答案
一卷搞定系列答案科目:高中數學 來源: 題型:
【題目】天干地支紀年法源于中國,中國自古便有十天干與十二地支,十天干即甲、乙、丙、丁、戊、己、庚、辛、壬、癸;十二地支即子、丑、寅、卯、辰、已、午、未、申、酉、戌、亥天干地支紀年法是按順序以一個天干和一個地支相配,排列起來,天干在前,地支在后,天干由“甲”起,地支由“子”起,例如,第一年為“甲子”,第二年為“乙丑”,第三年為“丙寅”,…,以此類推,排列到“癸酉”后,天于回到“甲”重新開始,即“甲戌”,“乙亥”,然后地支回到“子”重新開始,即“丙子”,以此類推已知1949年為“己丑”年,那么到中華人民共和國成立70年時為( )
A.丙酉年B.戊申年C.己申年D.己亥年
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,點![]() 是正方體
是正方體![]() 中的側面
中的側面![]() 上的一個動點,則下列結論正確的是( )
上的一個動點,則下列結論正確的是( )
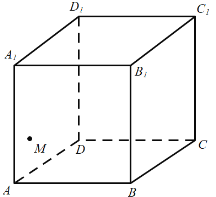
A.點![]() 存在無數個位置滿足
存在無數個位置滿足![]()
B.若正方體的棱長為1,三棱錐![]() 的體積最大值為
的體積最大值為![]()
C.在線段![]() 上存在點
上存在點![]() ,使異面直線
,使異面直線![]() 與
與![]() 所成的角是
所成的角是![]()
D.點![]() 存在無數個位置滿足到直線
存在無數個位置滿足到直線![]() 和直線
和直線![]() 的距離相等.
的距離相等.
查看答案和解析>>
科目:高中數學 來源: 題型:
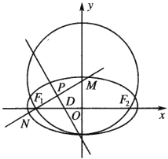
【題目】圓![]() 過橢圓
過橢圓![]() 的下頂點及左、右焦點
的下頂點及左、右焦點![]() ,
,![]() ,過橢圓
,過橢圓![]() 的左焦點
的左焦點![]() 的直線與橢圓
的直線與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,線段
兩點,線段![]() 的中垂線交
的中垂線交![]() 軸于點
軸于點![]() 且垂足為點
且垂足為點![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)證明:當直線![]() 斜率變化時
斜率變化時![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 右焦點與拋物線
右焦點與拋物線![]() 的焦點重合,以原點為圓心、橢圓短半軸長為半徑的圓與直線
的焦點重合,以原點為圓心、橢圓短半軸長為半徑的圓與直線![]() 相切.
相切.
(1)求橢圓的方程
(2)若直線![]() 與y軸交點為P,A、B是橢圓上兩個動點,它們在y軸兩側,
與y軸交點為P,A、B是橢圓上兩個動點,它們在y軸兩側,![]() ,
,![]() 的平分線與y軸重合,則直線AB是否過定點,若過定點,求這個定點坐標,若不過定點說明理由.
的平分線與y軸重合,則直線AB是否過定點,若過定點,求這個定點坐標,若不過定點說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦距為2,且過點
的焦距為2,且過點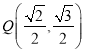 .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
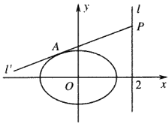
(2)若![]() 為坐標原點,
為坐標原點,![]() 為直線
為直線![]() 上的一動點,過點
上的一動點,過點![]() 作直線
作直線![]() 與橢圓相切于點
與橢圓相切于點![]() ,若
,若![]() 的面積
的面積![]() 為
為![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com