

 為“任意一個面上三個頂點不同色”,分析
為“任意一個面上三個頂點不同色”,分析 ,只需在正四面體的四個頂點先取兩個涂色,再將剩余的2個點涂上另一種顏色即可,可得其涂色方法數目,由等可能事件的概率可得P(
,只需在正四面體的四個頂點先取兩個涂色,再將剩余的2個點涂上另一種顏色即可,可得其涂色方法數目,由等可能事件的概率可得P( )=
)=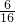 =
= ,根據對立事件概率之和為1,可得答案.
,根據對立事件概率之和為1,可得答案. 為“任意一個面上三個頂點不同色”,
為“任意一個面上三個頂點不同色”, ,只需在正四面體的四個頂點先取兩個涂色,再將剩余的點涂上另一種顏色即可,共
,只需在正四面體的四個頂點先取兩個涂色,再將剩余的點涂上另一種顏色即可,共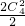 =6種,
=6種, )=
)=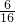 =
= ,
, =
= ;
; .
.

 培優三好生系列答案
培優三好生系列答案 優化作業上海科技文獻出版社系列答案
優化作業上海科技文獻出版社系列答案科目:高中數學 來源: 題型:
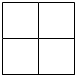 用紅、黃兩種顏色給圖中4個小正方形隨機涂色,每個小正方形只涂一種顏色,求:
用紅、黃兩種顏色給圖中4個小正方形隨機涂色,每個小正方形只涂一種顏色,求:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 用紅、黃兩種顏色給圖中4個小正方形隨機涂色,每個小正方形只涂一種顏色,求:
用紅、黃兩種顏色給圖中4個小正方形隨機涂色,每個小正方形只涂一種顏色,求:查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com