Question

【題目】已知函數(shù).

（1）求函數(shù)的單調(diào)區(qū)間；

（2）設(shè)函數(shù).當時，若函數(shù)在上為增函數(shù)，求實數(shù)的取值范圍.

Answer 1

【答案】(1) 在上單調(diào)遞減，在，上單調(diào)遞增.

(2) .

【解析】

（1）求導(dǎo)，根據(jù)正負討論導(dǎo)函數(shù)符號，確定對應(yīng)單調(diào)區(qū)間，（2）先利用導(dǎo)數(shù)研究正負，根據(jù)正負去絕對值將化為分段函數(shù)，再利用導(dǎo)數(shù)分段研究單調(diào)性，利用變量分離法轉(zhuǎn)化為求對應(yīng)函數(shù)最值問題，最后根據(jù)最值確定實數(shù)的取值范圍.

（1）對求導(dǎo)得

（i）若，當時，，當或時，

所以在上單調(diào)遞增，在，上單調(diào)遞減

（ii）若，當時，，當或時，

所以在上單調(diào)遞減，在，上單調(diào)遞增.

（2）記函數(shù)，

考察函數(shù)的符號

對函數(shù)求導(dǎo)得

當時，恒成立

當時，

從而

∴在上恒成立，故在上單調(diào)遞減.

∴

∴

又曲線在上連續(xù)不間斷，所以由函數(shù)的零點存在性定理及其單調(diào)性知

存在唯一的，使，

所以當時，，當時，

∴，∴

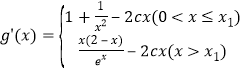
由上述討論過程可知曲線在上連續(xù)不斷，又函數(shù)為增函數(shù)

所以在上恒成立

①當時，在上恒成立，即在上恒成立，

記 ，，則，

當變化時，，變化情況如下表：

∴

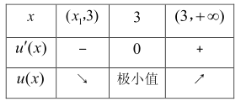
故“在上恒成立”只需，即

②當時，，

當時，在上恒成立

綜合①②，知當時，函數(shù)在為增函數(shù)

故實數(shù)的取值范圍是.