
分析 (1)根據導數的幾何意義,求得切線的斜率,利用點斜式方程,即可求得函數f(x)在x=1處的切線方程;
(2)求導,分類討論,根據導數與函數單調性及極值的關系,分別求得函數f(x)極值點的個數;
(3)方法一:由(2)可知:分類討論,根據函數的單調性,求得f(x)的最值,即可求得a的取值范圍;
方法二:設g(x)=2ax2-3ax+1,根據二次函數的性質,分類討論,即可求得實數a的取值范圍.
解答 解:(1)當a=0時,f(x)=lnx,f(1)=0,
求導f′(x)=$\frac{1}{x}$,f′(1)=1,
f(x)在x=1處的切線斜率k=1,則y-0=1×(x-1),整理得:y=x-1,;
∴函數f(x)在x=1處的切線方程y=x-1;…(3分)
(2)f(x)=lnx+a(x2-3x+2),定義域為(0,+∞)$f'(x)=\frac{1}{x}+a(2x-3)=\frac{{2a{x^2}-3ax+1}}{x}$,設g(x)=2ax2-3ax+1,
①當a=0時,g(x)=1,故f'(x)>0,
∴f(x)在(0,+∞)上為增函數,所以無極值點.…(4分)
②當a>0時,△=9a2-8a,
若0<a≤$\frac{8}{9}$時△≤0,g(x)≥0,故f'(x)≥0,故f(x)在(0,+∞)上遞增,所以無極值點.
若a>$\frac{8}{9}$時△>0,設g(x)=0的兩個不相等的實數根為x1,x2,且x1<x2,
且${x_1}+{x_2}=\frac{3}{2}$,而g(0)=1>0,則$0<{x_1}<\frac{3}{4}<{x_2}$,
所以當x∈(0,x1),g(x)>0,f'(x)>0,f(x)單調遞增;
當x∈(x1,x2),g(x)<0,f'(x)<0,f(x)單調遞減;
當x∈(x2,+∞),g(x)>0,f′(x)>0,f(x)單調遞增.
所以此時函數f(x)有兩個極值點;…(7分)
③當a<0時△>0,設g(x)=0的兩個不相等的實數根為x1,x2,且x1<x2,
但g(0)=1>0,所以x1<0<x2,
所以當x∈(0,x2),g(x)>0,f'(x)>0,f(x)單調遞増;
當x∈(x2,+∞),g(x)<0,f′(x)<0,f(x)單調遞減.
所以此時函數f(x)只有一個極值點.
綜上得:
當a<0時f(x)有一個極值點;
當0≤a≤$\frac{8}{9}$時f(x)的無極值點;
當a>$\frac{8}{9}$時,f(x)的有兩個極值點.…(9分)
(3)方法一:當0≤a≤$\frac{8}{9}$時,由(2)知f(x)在[1,+∞)上遞增,
所以f(x)≥f(1)=0,符合題意; …(10分)
當$\frac{8}{9}$<a≤1時,g(1)=1-a≥0,x2≤1,f(x)在[1,+∞)上遞增,所以f(x)≥f(1)=0,符合題意; …(12分)
當a>1時,g(1)=1-a<0,x2>1,所以函數f(x)在(1,x2)上遞減,所以f(x)<f(1)=0,不符合題意; …(14分)
當a<0時,由(1)知lnx≤x-1,于是f(x)=lnx+a(x2-3x+2)≤x-1+a(x2-3x+2)
當$x>2-\frac{1}{a}$時,x-1+a(x2-3x+2)<0,此時f(x)<0,不符合題意.
綜上所述,a的取值范圍是0≤a≤1.…(16分)
方法二:g(x)=2ax2-3ax+1,注意到對稱軸為$x=\frac{3}{4}$,g(1)=1-a,
當0≤a≤1時,可得g(x)≥0,故f(x)在[1,+∞)上遞增,所以f(x)≥f(1)=0,符合題意;
當a>1時,g(1)=1-a<0,x2>1,所以函數f(x)在(1,x2)上遞減,此時f(x)<f(1)=0,不符合題意;
當a<0時,由(1)知lnx≤x-1,于是f(x)=lnx+a(x2-3x+2)≤x-1+a(x2-3x+2)
當$x>2-\frac{1}{a}$時,x-1+a(x2-3x+2)<0,此時f(x)<0,不符合題意.
綜上所述,s的取值范圍是0≤a≤1.…(16分)
點評 本題考查導數的綜合應用,考查導數與函數單調性及極值的關系,考查二次函數的性質,考查分類討論思想,考查計算能力,屬于難題.


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
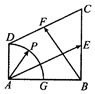 在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分別為BC,CD的中點,以A為圓心,AD為半徑的圓交AB于G,點P在$\widehat{DG}$上運動(如圖).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,則6λ+μ的取值范圍是( )
在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分別為BC,CD的中點,以A為圓心,AD為半徑的圓交AB于G,點P在$\widehat{DG}$上運動(如圖).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,則6λ+μ的取值范圍是( )| A. | [1,$\sqrt{2}$] | B. | [$\sqrt{2}$,2$\sqrt{2}$] | C. | [2,2$\sqrt{2}$] | D. | [1,2$\sqrt{2}$] |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,e) | B. | (1,+∞) | C. | (1,e) | D. | (e,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com