
【題目】函數f(x)=mx2﹣2x+1有且僅有一個為正實數的零點,則實數m的取值范圍是( )
A.(﹣∞,1]
B.(﹣∞,0]∪{1}
C.(﹣∞,0)∪(0,1]
D.(﹣∞,1)
科目:高中數學 來源: 題型:
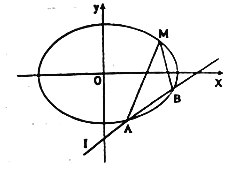
【題目】已知橢圓的中心在原點,焦點在![]() 軸上,離心率為
軸上,離心率為![]() ,且經過點
,且經過點![]() ,直線
,直線![]() :
: ![]() 交橢圓于
交橢圓于![]() ,
, ![]() 兩不同的點.
兩不同的點.
(1)求橢圓的方程;
(2)若直線![]() 不過點
不過點![]() ,求證:直線
,求證:直線![]() ,
, ![]() 與
與![]() 軸圍成等腰三角形.
軸圍成等腰三角形.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2x+k,且log2f(a)=2,f(log2a)=k,a>0,且a≠1.
(1)求a,k的值;
(2)當x為何值時,f(logax)有最小值?求出該最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下四個命題,其中正確的個數有( )
①由獨立性檢驗可知,有![]() 的把握認為物理成績與數學成績有關,某人數學成績優秀,則他有99%的可能物理優秀.
的把握認為物理成績與數學成績有關,某人數學成績優秀,則他有99%的可能物理優秀.
②兩個隨機變量相關性越強,則相關系數的絕對值越接近于1;
③在線性回歸方程![]() 中,當解釋變量
中,當解釋變量![]() 每增加一個單位時,預報變量
每增加一個單位時,預報變量![]() 平均增加0.2個單位;
平均增加0.2個單位;
④對分類變量![]() 與
與![]() ,它們的隨機變量
,它們的隨機變量![]() 的觀測值
的觀測值![]() 來說,
來說, ![]() 越小,“
越小,“![]() 與
與![]() 有關系”的把握程度越大.
有關系”的把握程度越大.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知下列命題:
①若![]() ,則“
,則“![]() ”是“
”是“![]() ”成立的充分不必要條件;
”成立的充分不必要條件;
②若橢圓![]() 的兩個焦點為
的兩個焦點為![]() ,且弦
,且弦![]() 過點
過點![]() ,則
,則![]() 的周長為16;
的周長為16;
③若命題“![]() ”與命題“
”與命題“![]() 或
或![]() ”都是真命題,則命題
”都是真命題,則命題![]() 一定是真命題;
一定是真命題;
④若命題![]() :
: ![]() ,則
,則![]() :
: ![]()
其中為真命題的是__________(填序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=log2 ![]() . (Ⅰ)判斷f(x)奇偶性并證明;
. (Ⅰ)判斷f(x)奇偶性并證明;
(Ⅱ)用單調性定義證明函數g(x)= ![]() 在函數f(x)定義域內單調遞增,并判斷f(x)=log2
在函數f(x)定義域內單調遞增,并判斷f(x)=log2 ![]() 在定義域內的單調性.
在定義域內的單調性.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若α∈[0,π],β∈[﹣ ![]() ,
, ![]() ],λ∈R,且(α﹣
],λ∈R,且(α﹣ ![]() )3﹣cosα﹣2λ=0,4β3+sinβcosβ+λ=0,則cos(
)3﹣cosα﹣2λ=0,4β3+sinβcosβ+λ=0,則cos( ![]() +β)的值為( )
+β)的值為( )
A.0
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C1,C2的極坐標方程分別為ρ=2cosθ, ![]() ,射線θ=φ,
,射線θ=φ, ![]() ,
, ![]() 與曲線C1交于(不包括極點O)三點A,B,C.
與曲線C1交于(不包括極點O)三點A,B,C.
(Ⅰ)求證: ![]() ;
;
(Ⅱ)當![]() 時,求點B到曲線C2上的點的距離的最小值.
時,求點B到曲線C2上的點的距離的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com