
【題目】設A,B分別是雙曲線![]() 的左右頂點,設過
的左右頂點,設過![]() 的直線PA,PB與雙曲線分別交于點M,N,直線MN交x軸于點Q,過Q的直線交雙曲線的于S,T兩點,且
的直線PA,PB與雙曲線分別交于點M,N,直線MN交x軸于點Q,過Q的直線交雙曲線的于S,T兩點,且![]() ,則
,則![]() 的面積( )
的面積( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 華東師大版一課一練系列答案
華東師大版一課一練系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中數學 來源: 題型:
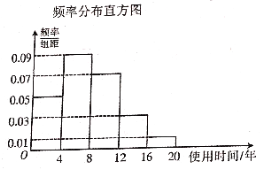
【題目】為了解一款電冰箱的使用時間和市民對這款電冰箱的購買意愿,研究人員對該款電冰箱進行了相應的抽樣調查,得到數據的統計圖表如下:
購買意愿市民年齡 | 不愿意購買該款電冰箱 | 愿意購買該款電冰箱 | 總計 |
40歲以上 | 600 | 800 | |
40歲以下 | 400 | ||
總計 | 800 |
(1)根據圖中的數據,估計該款電冰箱使用時間的中位數;
(2)完善表中數據,并據此判斷是否有![]() 的把握認為“愿意購買該款電冰箱“與“市民年齡”有關;
的把握認為“愿意購買該款電冰箱“與“市民年齡”有關;
(3)用頻率估計概率,若在該電冰箱的生產線上隨機抽取3臺,記其中使用時間不低于4年的電冰箱的臺數為![]() ,求
,求![]() 的期望.
的期望.
附:![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】住在同一城市的甲、乙兩位合伙人,約定在當天下午4:20-5:00間在某個咖啡館相見商談合作事宜,他們約好當其中一人先到后最多等對方10分鐘,若等不到則可以離去,則這兩人能相見的概率為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 上的點到右焦點F的最大距離為
上的點到右焦點F的最大距離為![]() ,離心率為
,離心率為![]() .
.
![]() 求橢圓C的方程;
求橢圓C的方程;
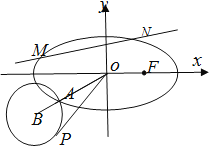
![]() 如圖,過點
如圖,過點![]() 的動直線l交橢圓C于M,N兩點,直線l的斜率為
的動直線l交橢圓C于M,N兩點,直線l的斜率為![]() ,A為橢圓上的一點,直線OA的斜率為
,A為橢圓上的一點,直線OA的斜率為![]() ,且
,且![]() ,B是線段OA延長線上一點,且
,B是線段OA延長線上一點,且![]() 過原點O作以B為圓心,以
過原點O作以B為圓心,以![]() 為半徑的圓B的切線,切點為
為半徑的圓B的切線,切點為![]() 令
令![]() ,求
,求![]() 取值范圍.
取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某科技創新公司在第一年年初購買了一臺價值昂貴的設備,該設備的第1年的維護費支出為20萬元,從第2年到第6年,每年的維修費增加4萬元,從第7年開始,每年維修費為上一年的125%.
(1)求第n年該設備的維修費![]() 的表達式;
的表達式;
(2)設![]() ,若
,若![]() 萬元,則該設備繼續使用,否則須在第n年對設備更新,求在第幾年必須對該設備進行更新?
萬元,則該設備繼續使用,否則須在第n年對設備更新,求在第幾年必須對該設備進行更新?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】4名運動員參加一次乒乓球比賽,每![]() 名運動員都賽
名運動員都賽![]() 場并決出勝負.設第
場并決出勝負.設第![]() 位運動員共勝
位運動員共勝![]() 場,負
場,負![]() 場
場![]() ,則錯誤的結論是( )
,則錯誤的結論是( )
A. ![]()
B. ![]()
C. ![]() 為定值,與各場比賽的結果無關
為定值,與各場比賽的結果無關
D. ![]() 為定值,與各場比賽結果無關
為定值,與各場比賽結果無關
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com