
【題目】已知函數![]() (其中
(其中![]() )
)
(1)求![]() 的單調減區間;
的單調減區間;
(2)當![]() 時,
時,![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)設![]()
![]() 只有兩個零點
只有兩個零點![]() (
(![]() ),求
),求![]() 的值.
的值.
【答案】(1)單調減區間為(-∞,0)和(0,1);(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求得函數的定義域,然后求導,利用導數求得函數的單調減區間.(2)構造函數![]() ,利用其二階導數研究它的單調性,由此求得
,利用其二階導數研究它的單調性,由此求得![]() 的取值范圍.(3)化簡
的取值范圍.(3)化簡![]() ,利用導數,研究
,利用導數,研究![]() 零點分布的情況,由此求得
零點分布的情況,由此求得![]() 的值.
的值.
(1)![]() 的定義域為{x|x≠0},
的定義域為{x|x≠0},
![]() =
=![]() <0,解得:x<1,
<0,解得:x<1,
所以,![]() 的單調減區間為(-∞,0)和(0,1)
的單調減區間為(-∞,0)和(0,1)
(2)“當![]() 時,
時,![]() 恒成立”等價于“當
恒成立”等價于“當![]() 時,
時,![]() 恒成立”,其中
恒成立”,其中![]() .構造函數
.構造函數![]() ,則
,則![]() .記
.記![]() ,則
,則![]() .
.
(i)若![]() ,則
,則![]() 在
在![]() 上恒成立,
上恒成立,![]() 在
在![]() 上單調遞增,因此當
上單調遞增,因此當![]() 時,有
時,有![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上單調遞增,因此當
上單調遞增,因此當![]() 時,有
時,有![]() ,即
,即![]() ,故
,故![]() 恒成立,符合題意.
恒成立,符合題意.
(ii)若![]() ,則
,則![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上單調遞減,因此當
上單調遞減,因此當![]() 時,有
時,有![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上單調遞減,因此
上單調遞減,因此![]() 時,有
時,有![]() ,即
,即![]() .故
.故![]() 不對任意
不對任意![]() 恒成立,不符合題意.綜上所述,
恒成立,不符合題意.綜上所述,![]() 的取值范圍是
的取值范圍是![]() .
.
(3)![]() ,所以
,所以![]() ,依題意知關于
,依題意知關于![]() 的方程
的方程![]() 只有兩個實數根
只有兩個實數根![]() ,即關于
,即關于![]() 的方程
的方程![]() 只有兩個非零實根
只有兩個非零實根![]() ,其中
,其中![]() .故
.故![]() ,或
,或![]() 或
或![]() .
.
(i)若![]() ,則
,則![]() ,不符合題意;
,不符合題意;
(ii)若![]() ,比較對應項系數,得
,比較對應項系數,得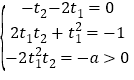 ,解得
,解得![]() .不滿足
.不滿足![]() ,故不符合題意;
,故不符合題意;
(iii)若![]() ,同理可得
,同理可得![]() ,符合題意,此時
,符合題意,此時![]() .綜上所述,
.綜上所述,![]() 的值為
的值為![]() .
.


科目:高中數學 來源: 題型:
【題目】直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,已知
兩點,已知![]()
![]() ,
,![]()
![]() ,若橢圓的離心率
,若橢圓的離心率![]() ,又經過點
,又經過點![]() ,
,![]() 為坐標原點.
為坐標原點.
(1)求橢圓的方程;
(2)當![]() 時,試問:
時,試問:![]() 的面積是否為定值?如果是,請給予證明;如果不是,請說明理由.
的面積是否為定值?如果是,請給予證明;如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (a>b>0)經過點
(a>b>0)經過點![]() ,且離心率為
,且離心率為![]() .
.
(Ⅰ)求橢圓C的方程;
(Ⅱ)已知A(0,b),B(a,0),點P是橢圓C上位于第三象限的動點,直線AP、BP分別將x軸、y軸于點M、N,求證:|AN||BM|為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個大型噴水池的中央有一個強力噴水柱,為了測量噴水柱噴出的水柱的高度,某人在噴水柱正西方向的點A測得水柱頂端的仰角為45°,沿點A向北偏東30°前進100 m到達點B,在B點測得水柱頂端的仰角為30°,則水柱的高度是( )
A. 50 mB. 100 m
C. 120 mD. 150 m
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一盒中裝有9張各寫有一個數字的卡片,其中4張卡片上的數字是1,3張卡片上的數字是2,2張卡片上的數字是3,從盒中任取3張卡片.
(1)求所取3張卡片上的數字完全相同的概率;
(2)![]() 表示所取3張卡片上的數字的中位數,求
表示所取3張卡片上的數字的中位數,求![]() 的分布列與數學期望.
的分布列與數學期望.
(注:若三個數![]() 滿足
滿足![]() ,則稱
,則稱![]() 為這三個數的中位數).
為這三個數的中位數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是中國古代第一部數學專著,成于公元一世紀左右,系統總結了戰國、秦、漢時期的數學成就.其中《方田》一章中記載了計算弧田(弧田就是由圓弧和其所對弦所圍成弓形)的面積所用的經驗公式:弧田面積=![]() (弦×矢+矢×矢),公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差.按照上述經驗公式計算所得弧田面積與其實際面積之間存在誤差.現有圓心角為
(弦×矢+矢×矢),公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差.按照上述經驗公式計算所得弧田面積與其實際面積之間存在誤差.現有圓心角為![]() ,弦長為
,弦長為![]() 的弧田.其實際面積與按照上述經驗公式計算出弧田的面積之間的誤差為( )平方米.(其中
的弧田.其實際面積與按照上述經驗公式計算出弧田的面積之間的誤差為( )平方米.(其中![]() ,
,![]() )
)
A. 15 B. 16 C. 17 D. 18
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P-ABC中,已知PC⊥BC,PC⊥AC,點E,F,G分別是所在棱的中點,則下面結論中錯誤的是 ( )

A.平面EFG∥平面PBC
B.平面EFG⊥平面ABC
C.∠BPC是直線EF與直線PC所成的角
D.∠FEG是平面PAB與平面ABC所成二面角的平面角
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學用“五點法”畫函數![]() 在某一個周期內的圖像時,列表并填入了部分數據,如下表:
在某一個周期內的圖像時,列表并填入了部分數據,如下表:
|
|
| |||
| 0 |
|
|
|
|
| 0 | 3 | 0 | 0 |
(1)請將上表數據補充完整,并寫出函數![]() 的解析式(直接寫出結果即可);
的解析式(直接寫出結果即可);
(2)根據表格中的數據作出![]() 在一個周期內的圖像;
在一個周期內的圖像;
(3)求函數![]() 在區間
在區間![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com