
曲線![]() 與直線
與直線![]() 有兩個交點時,實數k的取值范圍是 ( )
有兩個交點時,實數k的取值范圍是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 A【解析】析:要求的實數k的取值范圍即為直線l斜率的取值范圍,主要求出斜率的取值范圍,方法為:曲線y=1+
A【解析】析:要求的實數k的取值范圍即為直線l斜率的取值范圍,主要求出斜率的取值范圍,方法為:曲線y=1+ ![]() 表示以(0,1)為圓心,2為半徑的半圓,在坐標系中畫出相應的圖形,直線l與半圓有不同的交點,故抓住兩個關鍵點:當直線l與半圓相切時,圓心到直線的距離等于圓的半徑,利用點到直線的距離公式列出關于k的方程,求出方程的解得到k的值;當直線l過B點時,由A和B的坐標求出此時直線l的斜率,根據兩種情況求出的斜率得出k的取值范圍.
表示以(0,1)為圓心,2為半徑的半圓,在坐標系中畫出相應的圖形,直線l與半圓有不同的交點,故抓住兩個關鍵點:當直線l與半圓相切時,圓心到直線的距離等于圓的半徑,利用點到直線的距離公式列出關于k的方程,求出方程的解得到k的值;當直線l過B點時,由A和B的坐標求出此時直線l的斜率,根據兩種情況求出的斜率得出k的取值范圍.
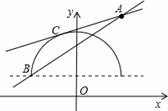
解答:解:根據題意畫出圖形,如圖所示:
由題意可得:直線l過A(2,4),B(-2,1),
又直線y=1+![]() 圖象為以(0,1)為圓心,2為半徑的半圓,
圖象為以(0,1)為圓心,2為半徑的半圓,
當直線l與半圓相切,C為切點時,圓心到直線l的距離d=r,即![]() =2,解得:k=
=2,解得:k=![]() ;當直線l過B點時,直線l的斜率為
;當直線l過B點時,直線l的斜率為![]() =
=![]() ,
,
則直線l與半圓有兩個不同的交點時,實數k的范圍為(![]() ,
,![]() ].故答案為:A
].故答案為:A


科目:高中數學 來源:2011-2012學年河北省高三下學期二調考試文科數學試卷(解析版) 題型:填空題
給出以下四個結論:
(1)若關于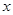 的方程
的方程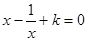 在
在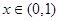 沒有實數根,則
沒有實數根,則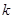 的取值范圍是
的取值范圍是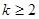
(2)曲線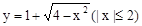 與直線
與直線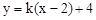 有兩個交點時,實數
有兩個交點時,實數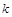 的取值范圍是
的取值范圍是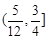
(3)已知點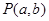 與點
與點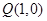 在直線
在直線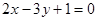 兩側, 則3b-2a>1;
兩側, 則3b-2a>1;
(4)若將函數 的圖像向右平移
的圖像向右平移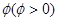 個單位后變為偶函數,則
個單位后變為偶函數,則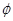 的最小值是
的最小值是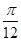 ;其中正確的結論是:__________________
;其中正確的結論是:__________________
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com