
(本小題滿分22分)
設A、B分別為橢圓![]()
![]() 和雙曲線
和雙曲線![]() 的公共的左、右頂點。P、Q分別為雙曲線和橢圓上不同于A、B的動點,且滿足
的公共的左、右頂點。P、Q分別為雙曲線和橢圓上不同于A、B的動點,且滿足![]()
![]() 。設直線AP、BP、AQ、BQ的斜率分別為k1、k2、k3、k4.
。設直線AP、BP、AQ、BQ的斜率分別為k1、k2、k3、k4.
(1)求證:k1+k2+k3+k4=0;
(2)設 F1、F2分別為橢圓和雙曲線的右焦點。若![]() ,求
,求![]() 的值。
的值。
解析:(1)設P、Q兩點的坐標分別為P(x1,y1),Q(x2,y2),則
k1+k2=![]() ①……………(4分)
①……………(4分)
同理可得意k3+k4=![]() ② …………………………(7分)
② …………………………(7分)
設O為原點,則![]() ,
,
所以![]() ,O,P,Q三點共線,于是得
,O,P,Q三點共線,于是得![]() .
.
由①②得 kl+k2+k3+k4=0; ………………………………………(11分)
(2) 由點Q在橢圓上,有![]() =1.
=1.
由 ![]() ,得(xl,y1)=
,得(xl,y1)=![]() (x2,y2).
(x2,y2).
所以 x2=![]() x l,y2=
x l,y2=![]() y l,從而
y l,從而![]() =
=![]() 2 ③
2 ③
又由點P在雙曲線上,有![]() =1 ④
=1 ④
由③④得 ![]() ……………………(15分)
……………………(15分)
因為PF2∥QF1,所以| OF2|=![]() |OF1| ,所以
|OF1| ,所以
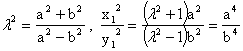 ………………………………(18分)
………………………………(18分)
由①得 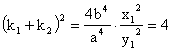 .同理可得
.同理可得 ![]() .另一方面,
.另一方面,
klk2=![]() .類似地,k3k4=
.類似地,k3k4=![]() .
.
故![]() -2(klk2+k3k4)=8 …(22分)
-2(klk2+k3k4)=8 …(22分)


 全優沖刺100分系列答案
全優沖刺100分系列答案 英才點津系列答案
英才點津系列答案科目:高中數學 來源: 題型:
(本小題滿分22分)
將m位性別相同的客人,按如下方法入住A1、A2、…、A n共n個房間。首先,安排1位客人和余下的客人![]() 的入住房間A1;然后,從余下的客人中安排2位和再次余下的客人
的入住房間A1;然后,從余下的客人中安排2位和再次余下的客人![]() 的入住房間A2;依此類推,第幾號房間就安排幾位客人和余下的客人
的入住房間A2;依此類推,第幾號房間就安排幾位客人和余下的客人![]() 的入住;這樣,最后一間房間A n正好安排最后余下的n位客人。試求客人的數目和客房的數目,以及每間客房入住客人的數目。
的入住;這樣,最后一間房間A n正好安排最后余下的n位客人。試求客人的數目和客房的數目,以及每間客房入住客人的數目。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年云南省高三第一次月考理科數學 題型:解答題
請考生在第22~24三題中任選一題作答,如果多做,則按所做的第一題記分.
(本小題滿分10分)選修4-1:幾何證明選講
如圖,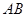 是⊙O的一條切線,切點為
是⊙O的一條切線,切點為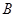 ,
,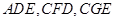 都是⊙O的割線,已知
都是⊙O的割線,已知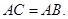 證明:
證明:
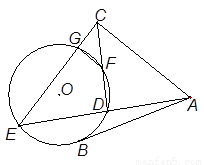
(Ⅰ)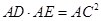 ;
;
(Ⅱ)
查看答案和解析>>
科目:高中數學 來源:2010-2011學年河南省鄭州市高三第一次質量預測數學理卷 題型:解答題
請考生在22、23兩題中任選一題作答,如果都做,則按所做的第一題記分。
(本小題滿分10分)選修4-1:幾何證明選講
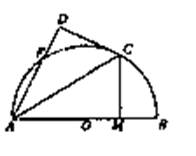
如圖,AB是⊙O的直徑,C、F為⊙O上的點,CA是∠BAF的角平分線,過點C
作CD⊥AF交AF的延長線于D點,CM⊥AB,垂足為點M。
(I)求證:DC是⊙O的切線; (II)求證:AM:MB=DF·DA。
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省汕頭市高三四校聯考數學理卷 題型:解答題
.(本小題滿分14分)
某校高三文科分為四個班.高三數學調研測試后, 隨機地在各班抽取部分學生進行測試成績統計,各班被抽取的學生人數恰好成等差數列,人數最少的班被抽取了22人. 抽取出來的所有學生的測試成績統計結果的頻率分布條形圖如圖5所示,其中120~130(包括120分但不包括130分)的頻率為0.05,此分數段的人數為5人.

(1) 問各班被抽取的學生人數各為多少人?
(2) 在抽取的所有學生中,任取一名學生, 求分數不小于90分的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com