
三棱錐S—ABC中,一條棱長為a,其余棱長均為1,求a為何值時VS—ABC最大,并求最大值.
a為![]() 時,三棱錐的體積最大為
時,三棱錐的體積最大為![]()
方法一 如圖所示,
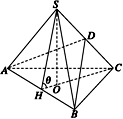 設SC=a,其余棱長均為1,
設SC=a,其余棱長均為1,
取AB的中點H,連接HS、HC,
則AB⊥HC,AB⊥HS,
∴AB⊥平面SHC.
在面SHC中,過S作SO⊥HC,則SO⊥平面ABC.
在△SAB中,SA=AB=BS=1,
∴SH=![]() ,
,
設∠SHO=![]() ,則SO=SHsin
,則SO=SHsin![]() =
=![]() sin
sin![]() ,
,
∴VS—ABC=![]() S△ABC·SO
S△ABC·SO
=![]() ×
×![]() ×12×
×12×![]() sin
sin![]()
=![]() sin
sin![]() ≤
≤![]() .
.
當且僅當sin![]() =1,即
=1,即![]() =90°時,三棱錐的體積最大.
=90°時,三棱錐的體積最大.
a=![]() SH=
SH=![]() ×
×![]() =
=![]() ,Vmax=
,Vmax=![]() .
.
∴a為![]() 時,三棱錐的體積最大為
時,三棱錐的體積最大為![]() .
.
方法二 取SC的中點D,可通過VS—ABC=![]() S△ABD·SC,轉化為關于a的目標函數的最大值問題,利用基本不等式或配方法解決.
S△ABD·SC,轉化為關于a的目標函數的最大值問題,利用基本不等式或配方法解決.


科目:高中數學 來源: 題型:
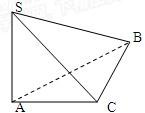 如圖在三棱錐S-ABC中∠ACB=90°,SA⊥面ABC,AC=2,BC=
如圖在三棱錐S-ABC中∠ACB=90°,SA⊥面ABC,AC=2,BC=| 13 |
| 29 |
查看答案和解析>>
科目:高中數學 來源: 題型:
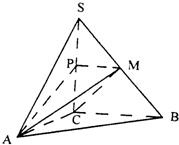 如圖,在三棱錐S-ABC中,SC⊥平面ABC,點P、M分別是SC和SB的中點,設PM=AC=1,∠ACB=90°,直線AM與直線SC所成的角為60°.
如圖,在三棱錐S-ABC中,SC⊥平面ABC,點P、M分別是SC和SB的中點,設PM=AC=1,∠ACB=90°,直線AM與直線SC所成的角為60°.查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在三棱錐S-ABC中,△ABC是邊長為8的正三角形,SA=SC=2
如圖,在三棱錐S-ABC中,△ABC是邊長為8的正三角形,SA=SC=2| 7 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在三棱錐S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如圖,在三棱錐S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com