
(本題滿分13分)
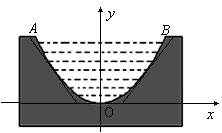
一個截面為拋物線形的舊河道(如圖1),河口寬![]() 米,河深2米,現要將其截面改造為等腰梯形(如圖2),要求河道深度不變,而且施工時只能挖土,不準向河道填土.
米,河深2米,現要將其截面改造為等腰梯形(如圖2),要求河道深度不變,而且施工時只能挖土,不準向河道填土.
(Ⅰ)建立恰當的直角坐標系并求出拋物線弧![]() 的標準方程;
的標準方程;
(Ⅱ)試求當截面梯形的下底(較長的底邊)長為多少米時,才能使挖出的土最少?

解:(1)如圖:以拋物線的頂點為原點,
![]() 中垂線為
中垂線為![]() 軸建立直角坐標系------1分
軸建立直角坐標系------1分
 則
則![]() ------2分
------2分
設拋物線的方程為![]() ,將點
,將點![]() 代入得
代入得![]() -------3分
-------3分
所以拋物線弧AB方程為![]() (
(![]() ) ------4分
) ------4分
(2)解法一:
設等腰梯形的腰與拋物線相切于![]()
![]()
則過![]() 的切線
的切線![]() 的斜率為
的斜率為![]()
所以切線![]() 的方程為:
的方程為:![]() ,即
,即![]()
令![]() ,得
,得![]() , 令
, 令![]() ,得
,得![]() ,
,
所以梯形面積![]() -----10分
-----10分
當僅當![]() ,即
,即![]() 時,
時,![]() 成立
成立
此時下底邊長為![]() -----12分
-----12分
答:當梯形的下底邊長等于![]() 米時,挖出的土最少. -----13分
米時,挖出的土最少. -----13分
解法二:設等腰梯形的腰與拋物線相切于![]()
![]()
則過![]() 的切線
的切線![]() 的斜率為
的斜率為![]()
所以切線![]() 的方程為:
的方程為:![]() ,即
,即![]()
運用定積分計算拋物線與等腰梯形間的面積:
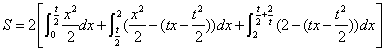 -----10分
-----10分
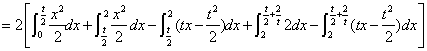
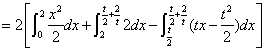
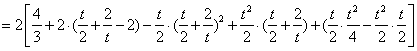
![]()
![]()
當僅當![]() ,即
,即![]() 時,
時,![]() 成立,此時下底邊長為
成立,此時下底邊長為![]() ---12分
---12分
答:當梯形的下底邊長等于![]() 米時,挖出的土最少. -----------13分
米時,挖出的土最少. -----------13分
解法三:設等腰梯形上底(較短的邊)長為![]() 米,則一腰過點
米,則一腰過點![]() ,可設此腰所在直線方程為
,可設此腰所在直線方程為![]() , 聯立
, 聯立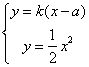 ,得
,得![]() ,
,
令![]() ,得
,得![]() ,或
,或![]() (舍),
(舍),
故此腰所在直線方程為![]() ,
,
令![]() ,得
,得![]() ,
,
故等腰梯形的面積:![]() ------------10分
------------10分
當且僅當![]() ,即
,即![]() 時,有
時,有![]()
此時,下底邊長![]() ------------12分
------------12分
答:當梯形的下底邊長等于![]() 米時,挖出的土最少. ----------13分
米時,挖出的土最少. ----------13分


 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:高中數學 來源:2012屆浙江省寧波萬里國際學校高三上期中理科數學試卷(解析版) 題型:解答題
(本題滿分13分) 的三個內角
的三個內角 依次成等差數列.
依次成等差數列.
(Ⅰ)若 ,試判斷
,試判斷 的形狀;
的形狀;
(Ⅱ)若 為鈍角三角形,且
為鈍角三角形,且 ,求
,求
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年北京市朝陽區高三上學期期末考試理科數學 題型:解答題
(本題滿分13分)
在銳角 中,
中, ,
, ,
, 分別為內角
分別為內角 ,
, ,
, 所對的邊,且滿足
所對的邊,且滿足 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,且
,且 ,
, ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年福建省龍巖市高三上學期期末考試數學理卷(一級學校) 題型:解答題
(本題滿分13分)
如圖,在五面體ABCDEF中,FA 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD,AF=AB=BC=FE=
AD,AF=AB=BC=FE= AD.
AD.
(Ⅰ)求異面直線BF與DE所成角的余弦值;
(Ⅱ)在線段CE上是否存在點M,使得直線AM與平面CDE所成角的正弦值為 ?若存在,試確定點M的位置;若不存在,請說明理由.
?若存在,試確定點M的位置;若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com