
【題目】將函數f(x)=cos(ωx+φ)(ω>0,|φ|< ![]() )的圖象上的每一點的縱坐標不變,橫坐標縮短為原來的一半,再將圖象向右平移
)的圖象上的每一點的縱坐標不變,橫坐標縮短為原來的一半,再將圖象向右平移 ![]() 個單位長度得到函數y=sinx的圖象.
個單位長度得到函數y=sinx的圖象.
(1)直接寫出f(x)的表達式,并求出f(x)在[0,π]上的值域;
(2)求出f(x)在[0,π]上的單調區間.
【答案】
(1)解:由題意可得,把函數y=sinx的圖象向左平移 ![]() 個單位長度得到y=sin(x+
個單位長度得到y=sin(x+ ![]() )的圖象,
)的圖象,
再把橫坐標縮短為原來的2倍,可得y=sin( ![]() x+
x+ ![]() )=cos[
)=cos[ ![]() ﹣(
﹣( ![]() x+
x+ ![]() )]=cos(
)]=cos( ![]() x﹣
x﹣ ![]() )的圖象,
)的圖象,
∴ ![]() .
.
∵0≤x≤π,∴ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,
當x=0時, ![]() ;當
;當 ![]() 時,f(x)=1
時,f(x)=1
(2)解:令 ![]() ,k∈Z,解得
,k∈Z,解得 ![]() ,k∈Z,
,k∈Z,
所以單調遞增區間為 ![]() ,k∈Z;
,k∈Z;
同理單調遞減區間為 ![]() ,k∈Z,
,k∈Z,
∵x∈[0,π],∴f(x)的單調遞增區間為 ![]() ,單調遞減區間為
,單調遞減區間為 ![]()
【解析】(1)利用函數y=Asin(ωx+φ)的圖象變換規律,正弦函數的定義域和值域,得出結論.(2)根據f(x)的解析式,以及正弦函數的單調性,得出結論.
【考點精析】解答此題的關鍵在于理解函數y=Asin(ωx+φ)的圖象變換的相關知識,掌握圖象上所有點向左(右)平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的橫坐標伸長(縮短)到原來的
的圖象上所有點的橫坐標伸長(縮短)到原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的縱坐標伸長(縮短)到原來的
的圖象上所有點的縱坐標伸長(縮短)到原來的![]() 倍(橫坐標不變),得到函數
倍(橫坐標不變),得到函數![]() 的圖象.
的圖象.


 53天天練系列答案
53天天練系列答案科目:高中數學 來源: 題型:
【題目】設函數f(x)=2sin(2x+φ)(0<φ<π),y=f(x)圖象的一個對稱中心是 ![]() .
. 
(1)求φ;
(2)在給定的平面直角坐標系中作出該函數在x∈[0,π]的圖象;
(3)求函數f(x)≥1(x∈R)的解集.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為研究患肺癌與是否吸煙有關,做了一次相關調查,其中部分數據丟失,但可以確定的是不吸煙人數與吸煙人數相同,吸煙患肺癌人數占吸煙總人數的![]() ;不吸煙的人數中,患肺癌與不患肺癌的比為
;不吸煙的人數中,患肺癌與不患肺癌的比為![]() .
.
(1)若吸煙不患肺癌的有![]() 人,現從患肺癌的人中用分層抽樣的方法抽取
人,現從患肺癌的人中用分層抽樣的方法抽取![]() 人,再從這
人,再從這![]() 人中隨機抽取
人中隨機抽取![]() 人進行調查,求這兩人都是吸煙患肺癌的概率;
人進行調查,求這兩人都是吸煙患肺癌的概率;
(2)若研究得到在犯錯誤概率不超過![]() 的前提下,認為患肺癌與吸煙有關,則吸煙的人數至少有多少?
的前提下,認為患肺癌與吸煙有關,則吸煙的人數至少有多少?
附: 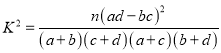 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將參加數學競賽的1000名學生編號如下:0001,0002,0003,…,1000,按系統抽樣的方法從中抽取一個容量為50的樣本,如果在第一組抽得的編號是0015,則在第21組抽得的編號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一家面包房根據以往某種面包的銷售記錄,繪制了日銷售量的頻率分布直方圖,如圖所示.將日銷售量落入各組的頻率視為概率. 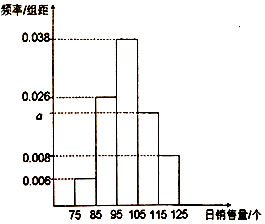
(1)求a的值并估計在一個月(按30天算)內日銷售量不低于105個的天數;
(2)利用頻率分布直方圖估計每天銷售量的平均值及方差(同一組中的數據用該組區間的中點值作代表).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某教師調查了![]() 名高三學生購買的數學課外輔導書的數量,將統計數據制成如下表格:
名高三學生購買的數學課外輔導書的數量,將統計數據制成如下表格:
男生 | 女生 | 總計 | |
購買數學課外輔導書超過 |
|
|
|
購買數學課外輔導書不超過 |
|
|
|
總計 |
|
|
|
(Ⅰ)根據表格中的數據,是否有![]() 的把握認為購買數學課外輔導書的數量與性別相關;
的把握認為購買數學課外輔導書的數量與性別相關;
(Ⅱ)從購買數學課外輔導書不超過![]() 本的學生中,按照性別分層抽樣抽取
本的學生中,按照性別分層抽樣抽取![]() 人,再從這
人,再從這![]() 人中隨機抽取
人中隨機抽取![]() 人詢問購買原因,求恰有
人詢問購買原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com