
【題目】若不等式![]() 在(0,+∞)上恒成立,則a的取值范圍是________.
在(0,+∞)上恒成立,則a的取值范圍是________.
【答案】[![]() ,+∞)
,+∞)
【解析】設![]() ,則
,則![]() ,(i)當a≤0時,
,(i)當a≤0時, ![]() ,則
,則![]() 在(0,+∞)上單調遞增,所以
在(0,+∞)上單調遞增,所以![]() 在(0,+∞)上恒成立,與已知不符,故a≤0不符合題意.
在(0,+∞)上恒成立,與已知不符,故a≤0不符合題意.
(jj )當 a>0 時,令![]() ,
, ![]() ,且
,且![]() ,①當2a≥1,即
,①當2a≥1,即![]() 時,
時, ![]() ,于是
,于是![]() 在 (0,+∞)上單調遞減,所以
在 (0,+∞)上單調遞減,所以![]() ,即
,即![]() 在
在![]() 上成立.則f(x)在
上成立.則f(x)在![]() 上單調遞減,故f(x)< f (0)=0在(0,+∞)上成立,符合題意.②當0<2a<1,即0<a<
上單調遞減,故f(x)< f (0)=0在(0,+∞)上成立,符合題意.②當0<2a<1,即0<a<![]() 時,
時, ![]() ,
, 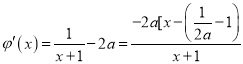 ,若
,若![]() ,則
,則![]() ,
, ![]() 在
在![]() 上單調遞増;若在
上單調遞増;若在![]() ,則
,則![]() ,
, ![]() 在
在![]() 上單調遞減,又
上單調遞減,又![]() ,則
,則![]() 在
在![]() 上成立,即
上成立,即![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上單調遞增,則
上單調遞增,則![]() 在
在![]() 上恒成立.與已知不符,故0<a<
上恒成立.與已知不符,故0<a<![]() 不符合題意.綜上所述,a的取值范圍[
不符合題意.綜上所述,a的取值范圍[![]() ,+∞).
,+∞).
故答案為[![]() ,+∞).
,+∞).


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】一個盒子中裝有6個完全相同的小球,分別標號為1,2,3,4,5,6.
(1)一次取出兩個小球,求其號碼之和能被3整除的概率;
(2)有放回的取球兩次,每次取一個,求兩個小球號碼是相鄰整數的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在空間中,下列命題正確的是
A.如果一個角的兩邊和另一角的兩邊分別平行,那么這兩個角相等
B.兩條異面直線所成的有的范圍是![]()
C.如果兩個平行平面同時與第三個平面相交,那么它們的交線平行
D.如果一條直線和平面內的一條直線平行,那么這條直線和這個平面平行
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的質量以其“無故障使用時間![]() (單位:小時)”衡量,無故障使用時間越大表明產品質量越好,且無故障使用時間大于3小時的產品為優質品,從某企業生產的這種產品中抽取100件,并記錄了每件產品的無故障使用時間,得到下面試驗結果:
(單位:小時)”衡量,無故障使用時間越大表明產品質量越好,且無故障使用時間大于3小時的產品為優質品,從某企業生產的這種產品中抽取100件,并記錄了每件產品的無故障使用時間,得到下面試驗結果:
無故障使用時間 |
|
|
|
頻數 | 20 | 40 | 40 |
以試驗結果中無故障使用時間落入各組的頻率作為一件產品的無故障使用時間落入相應組的概率.
(1)從該企業任取兩件這種產品,求至少有一件是優質品的概率;
(2)若該企業生產的這種產品每件銷售利潤![]() (單位:元)與其無故障使用時間
(單位:元)與其無故障使用時間![]() 的關系式為
的關系式為
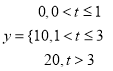
從該企業任取兩件這種產品,其利潤記為![]() (單位:元),求
(單位:元),求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
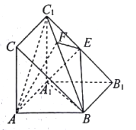
【題目】如圖,直三棱柱ABC—A1B1C1中,側面AA1B1B是正方形,AC丄側面AA1B1B,AC=AB,點E是B1C1的中點.
(Ⅰ)求證:C1A∥平面EBA1;
(Ⅱ)若EF丄BC1,垂足為F,求二面角B—AF—A1的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4—4:坐標系與參數方程]
在平面直角坐標系xOy中,直線l的參數方程為 (t為參數),以平面直角坐標系的原點為極點,正半軸為極軸,取相同的長度單位建立極坐標系,曲線C的極坐標方程為
(t為參數),以平面直角坐標系的原點為極點,正半軸為極軸,取相同的長度單位建立極坐標系,曲線C的極坐標方程為![]() .
.
(Ⅰ)求直線l和曲線C的直角坐標方程,并指明曲線C的形狀;
(Ⅱ)設直線l與曲線C交于A,B兩點,O為坐標原點,且|OA|<|OB|,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在![]() 中,內角
中,內角![]() 、
、![]() 、
、![]() 所對的邊分別是
所對的邊分別是![]() 、
、![]() 、
、![]() ,不等式
,不等式![]() 對一切實數
對一切實數![]() 恒成立.
恒成立.
(1)求![]() 的取值范圍;
的取值范圍;
(2)當![]() 取最大值,且
取最大值,且![]() 的周長為
的周長為![]() 時,求
時,求![]() 面積的最大值,并指出面積取最大值時
面積的最大值,并指出面積取最大值時![]() 的形狀.(參考知識:已知
的形狀.(參考知識:已知![]() 、
、![]() ,
,![]() ;
;![]() 、
、![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中錯誤的個數是( )
①從某社區65戶高收入家庭,280戶中等收入家庭,105戶低收入家庭中選出100戶調查社會購買力的某一項指標,應采用的最佳抽樣方法是分層抽樣
②線性回歸直線![]() 一定過樣本中心點
一定過樣本中心點![]()
③對于一組數據![]() ,如果將它們改變為
,如果將它們改變為![]() ,則平均數與方差均發生變化
,則平均數與方差均發生變化
④若一組數據1、![]() 、2、3的眾數是2,則這組數據的中位數是2
、2、3的眾數是2,則這組數據的中位數是2
⑤用系統抽樣方法從編號為1,2,3,…,700的學生中抽樣50人,若第2段中編號為20的學生被抽中,按照等間隔抽取的方法,則第5段中被抽中的學生編號為76
A.0B.1C.2D.3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com