
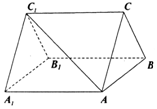
 如圖所示的三棱柱中,側面ABB1A1為邊長等于2的菱形,且∠AA1B1=60°,△ABC為等邊三角形,面ABC⊥面ABB1A1.
如圖所示的三棱柱中,側面ABB1A1為邊長等于2的菱形,且∠AA1B1=60°,△ABC為等邊三角形,面ABC⊥面ABB1A1.分析 (1)取A1B1的中點O,連結OA,OC1,只證A1B1面AOC1即可得到A1B1⊥AC1.
(2)先證明AO⊥AC1.再以O為坐標原點,OA1,OA,OC1方向為x、y、z軸建立坐標系O-xyz. 求出平面A1ACC1、平面BCAC1B1的法向量即可
解答  解:(1)證明:取A1B1的中點O,連結OA,OC1,
解:(1)證明:取A1B1的中點O,連結OA,OC1,
因為,△ABC為等邊三角形,∴C1O⊥A1B1,
在△A1AO中,A1A=2,A1O=1,∠AA1B1=60°,可得OA⊥OA1,
∴A1B1⊥C1O,A1B1⊥OA,OA∩OC1=O,∴${A}_{1}{B}_{1}⊥\\;面AO{C}_{1}$面AOC1
而AC1?面AOC1,A1B1⊥AC1.
(2)∵面A1B1C1⊥面ABB1A1,面A1B1C1∩面ABB1A1=B1A1,且C1O⊥A1B1,∴C1O⊥面ABB1A1,
OA?面ABB1A1∴AO⊥AC1.
由(1)知OA⊥OA1,OA1⊥OC1,故可以O為坐標原點,OA1,OA,OC1方向為x、y、z軸建立坐標系O-xyz.
A1(1,0,0),A(0,$\sqrt{3}$,0),C1(0,0,$\sqrt{3}$),B1(-1,0,0),C(-1,$\sqrt{3},\sqrt{3})$,
$\overrightarrow{{A}_{1}{C}_{1}}=(-1,0,\sqrt{3}),\overrightarrow{A{C}_{1}}=(0,-\sqrt{3},\sqrt{3})$,
設$\overrightarrow{m}=(x,y,z)$為平面A1ACC1的法向量,則$\left\{\begin{array}{l}{-x+\sqrt{3}z=0}\\{-\sqrt{3}y+\sqrt{3}z=0}\end{array}\right.$,可得$\overrightarrow{m}=(\sqrt{3},1,1)$.
$\overrightarrow{{B}_{1}{C}_{1}}=(1,0,\sqrt{3}),\overrightarrow{{C}_{1}C}=(-1,\sqrt{3},0)$.
設$\overrightarrow{n}=(a,b,c)$為平面BCAC1B1的法向量,則$\left\{\begin{array}{l}{a+\sqrt{3}c=0}\\{-a+\sqrt{3}b=0}\end{array}\right.$,可得$\overrightarrow{n}=(\sqrt{3},1,-1)$.
∴$cos<\overrightarrow{m},\overrightarrow{n}>=\frac{3}{5}$,
側面A1ACC1和側面BCC1B1所成的二面角的余弦值為$\frac{3}{5}$.
點評 本題考查了線線垂直的判定,向量法求二面角,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| A組 | B組 | 合計 | |
| 男性 | 26 | 24 | 50 |
| 女性 | 30 | 20 | 50 |
| 合計 | 56 | 44 | 100 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 喜歡游泳 | 不喜歡游泳 | 合計 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合計 | 60 | 40 | 100 |
| P(Χ2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{9}{16}$ | D. | $\frac{5}{16}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com