Question

設f（x）=log_n+1（n+2）（n∈N^*）．
（Ⅰ）求f（1）•f（2）和f（1）•f（2）•f（3）•f（4）•f（5）•f（6）的值；
（Ⅱ）若把使f（1）•f（2）•…•f（k）為整數的正整數k叫做企盼數，試求f（1）•f（2）•…•f（k）=2008的企盼數k．

Answer 1

解：（Ⅰ）因為f（x）=log_n+1（n+2），所以求f（1）•f（2）=．
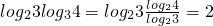
f（1）•f（2）•f（3）•f（4）•f（5）•f（6）=log?₂3?log?₃4?log?₄5?log?₅6?log?₆7?log?₇8=log?₂8=3．
（Ⅱ）由對數的換底公式得f（1）•f（2）•…•f（k）=log?₂（k+2），
由log?₂（k+2）=2008得k=2²⁰⁰⁸-2．
分析：（Ⅰ）利用對數的運算法則和換底公式求f（1）•f（2）和f（1）•f（2）•f（3）•f（4）•f（5）•f（6）的值；
（Ⅱ）關鍵企盼數的定義，求k．
點評：本題主要考查對數的運算以及對數的換底公式，要求熟練掌握對數的換底公式，考查學生的運算能力．
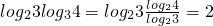