
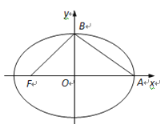
【題目】如圖,在平面直角坐標系xOy中,橢圓![]()
![]() 的左焦點為
的左焦點為![]() ,右頂點為
,右頂點為![]() ,上頂點為
,上頂點為![]() .
.
(1)已知橢圓的離心率為![]() ,線段
,線段![]() 中點的橫坐標為
中點的橫坐標為![]() ,求橢圓的標準方程;
,求橢圓的標準方程;
(2)已知△![]() 外接圓的圓心在直線
外接圓的圓心在直線![]() 上,求橢圓的離心率
上,求橢圓的離心率![]() 的值.
的值.
 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖(1),等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別是
分別是![]() 的兩個三等分點,若把等腰梯形沿虛線
的兩個三等分點,若把等腰梯形沿虛線![]() 、
、![]() 折起,使得點
折起,使得點![]() 和點
和點![]() 重合,記為點
重合,記為點![]() , 如圖(2).
, 如圖(2).

(1)求證:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設P是橢圓![]() 上一點,M,N分別是兩圓(x+4)2+y2=1和(x-4)2+y2=1上的點,則|PM|+|PN|的最小值、最大值分別為 ( )
上一點,M,N分別是兩圓(x+4)2+y2=1和(x-4)2+y2=1上的點,則|PM|+|PN|的最小值、最大值分別為 ( )
A. 9,12 B. 8,11 C. 10,12 D. 8,12
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() .數列
.數列![]() 滿足
滿足![]() ,
,![]() .
.
(1)若![]() ,且
,且![]() ,求正整數
,求正整數![]() 的值;
的值;
(2)若數列![]() ,
,![]() 均是等差數列,求
均是等差數列,求![]() 的取值范圍;
的取值范圍;
(3)若數列![]() 是等比數列,公比為
是等比數列,公比為![]() ,且
,且![]() ,是否存在正整數
,是否存在正整數![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差數列,若存在,求出一個
成等差數列,若存在,求出一個![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市政府為了節約生活用電,計劃在本市試行居民生活用電定額管理,即確定一戶居民月用電量標準a,用電量不超過a的部分按平價收費,超出a的部分按議價收費![]() 為此,政府調查了100戶居民的月平均用電量
為此,政府調查了100戶居民的月平均用電量![]() 單位:度
單位:度![]() ,以
,以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分組的頻率分布直方圖如圖所示.
分組的頻率分布直方圖如圖所示.
![]() 根據頻率分布直方圖的數據,求直方圖中x的值并估計該市每戶居民月平均用電量
根據頻率分布直方圖的數據,求直方圖中x的值并估計該市每戶居民月平均用電量![]() 的值;
的值;
![]() 用頻率估計概率,利用
用頻率估計概率,利用![]() 的結果,假設該市每戶居民月平均用電量X服從正態分布
的結果,假設該市每戶居民月平均用電量X服從正態分布![]()
![]() 估計該市居民月平均用電量介于
估計該市居民月平均用電量介于![]() 度之間的概率;
度之間的概率;
![]() 利用
利用![]() 的結論,從該市所有居民中隨機抽取3戶,記月平均用電量介于
的結論,從該市所有居民中隨機抽取3戶,記月平均用電量介于![]() 度之間的戶數為
度之間的戶數為![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)已知兩個變量線性相關,若它們的相關性越強,則相關系數的絕對值越接近于1.
(2)線性回歸直線必過點![]() ;
;
(3)對于分類變量A與B的隨機變量![]() ,
,![]() 越大說明“A與B有關系”的可信度越大.
越大說明“A與B有關系”的可信度越大.
(4)在刻畫回歸模型的擬合效果時,殘差平方和越小,相關指數![]() 的值越大,說明擬合的效果越好.
的值越大,說明擬合的效果越好.
(5)根據最小二乘法由一組樣本點![]() ,求得的回歸方程是
,求得的回歸方程是![]() ,對所有的解釋變量
,對所有的解釋變量![]() ,
,![]() 的值一定與
的值一定與![]() 有誤差.
有誤差.
以上命題正確的序號為____________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在底面是菱形的四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 在
在![]() 上,且
上,且![]() .
.
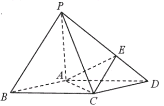
(1)證明:![]() 面
面![]() ;
;
(2)在棱![]() 上是否存在一點
上是否存在一點![]() ,使三棱錐
,使三棱錐![]() 是正三棱錐?證明你的結論.
是正三棱錐?證明你的結論.
(3)求以![]() 為棱,
為棱,![]() 與
與![]() 為面的二面角
為面的二面角![]() 的大小.
的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com