已知對任意平面向量
＝(x，y)，把繞其起點沿逆時針方向旋轉
角得到向量
＝(xcos－ysin，xsin＋ycos)，叫做把點B繞點A逆時針方向旋轉角得到點P．設平面內曲線C上的每一點繞原點沿逆時針方向旋轉
后得到點的軌跡是曲線x2＋y2＝2，則原來曲線C的方程是________
科目：高中數學 來源：陜西省漢中地區2007－2008學年度高三數學第一學期期中考試試卷(理科) 題型：044
在直角坐標平面中，已知點P1(1，2)，P2(2，22)，…pn(n，2n)，其中n是正整數．對平面上任一點A0，記A1為A0關于點P1的對稱點，A2為A1關于點P2的對稱點，…，AN為AN－1關于點PN的對稱點．
(1)求向量
的坐標；
(2)當點A0在曲線C上移動時，點A2的軌跡是函數y＝f(x)的圖象，其中f(x)是以3為周期的周期函數，且當x∈(0，3)時，f(x)＝lgx．求以曲線C為圖象的函數在(1，4)上的解析式；
(3)對任意偶數n，用n表示向量
的坐標．
查看答案和解析>>
科目：高中數學 來源：廣東省普寧二中2011－2012學年高二11月月考數學理科試題 題型：044
已知對任意的平面向量，把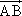
繞其起點沿逆時針方向旋轉
角，得到向量
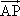＝(xcos－ysin，xsin＋ycos)，叫做把點B繞點A逆時針方向旋轉角得到點P
①已知平面內的點A(1，2)，B
，把點B繞點A沿逆時針方向旋轉
后得到點P，求點P的坐標
②設平面內曲線C上的每一點繞逆時針方向旋轉
后得到的點的軌跡是曲線x2－y2＝1，求原來曲線C的方程．
查看答案和解析>>
科目：高中數學 來源：2009年高考數學理科(四川卷) 題型：022
設V是已知平面M上所有向量的集合，對于映射f：→V，a∈V，記a的象為f(a)．若映射f：V→V滿足：對所有a，b∈V及任意實數λ，μ都有f(λa＋μb)＝λf(a)＋μf(b)，則f稱為平面M上的線性變換．現有下列命題：
①設f是平面M上的線性變換，則f(0)＝0
②對a∈V，設f(a)＝2a，則f是平面M上的線性變換；
③若e是平面M上的單位向量，對a∈V，設f(a)＝a－e，則f是平面M上的線性變換；
④設f是平面M上的線性變換，a，b∈V，若a，b共線，則f(a)，f(b)也共線．
其中真命題是________(寫出所有真命題的序號)
查看答案和解析>>
科目：高中數學 來源：2013-2014學年安徽省合肥市高三第一次教學質量檢測文科數學試卷（解析版） 題型：填空題
有下列命題：
①已知
是平面內兩個非零向量，則平面內任一向量
都可表示為
，其中
；
②對任意平面四邊形ABCD，點E、F分別為AB、CD的中點，則
；
③直線
的一個方向向量為
；
④已知
與
夾角為
，且·＝
，則｜－｜的最小值為
；
⑤
是（·）·
＝
·（
·
）的充分條件；
其中正確的是 （寫出所有正確命題的編號）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
