
【題目】已知函數![]() ,
,![]() ,其中
,其中![]() .
.
(1)若函數![]() 的圖象均在
的圖象均在![]() 軸上方,求
軸上方,求![]() 的取值范圍;
的取值范圍;
(2)記![]() 為函數
為函數![]() 在
在![]() 上的零點,若存在唯一的
上的零點,若存在唯一的![]() ,使得
,使得![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)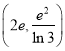 .
.
【解析】
(1)由題意可知,不等式![]() 對任意的
對任意的![]() 恒成立,利用導數求出函數
恒成立,利用導數求出函數![]() 的最小值,可得出關于實數
的最小值,可得出關于實數![]() 的不等式,即可求得實數
的不等式,即可求得實數![]() 的取值范圍;
的取值范圍;
(2)先利用“![]() 為函數
為函數![]() 在
在![]() 上的零點”得到
上的零點”得到![]() 的取值范圍,并得到結論
的取值范圍,并得到結論![]() ,然后利用另一個條件,再次得到
,然后利用另一個條件,再次得到![]() 的取值范圍,其中涉及隱零點問題,最后綜合兩次所得
的取值范圍,其中涉及隱零點問題,最后綜合兩次所得![]() 的取值范圍求出結果.
的取值范圍求出結果.
(1)由題意可得不等式![]() 對任意的
對任意的![]() 恒成立,則
恒成立,則![]() ,
,
![]() ,則
,則![]() ,令
,令![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
| 極小值 |
|
所以,函數![]() 的單調遞減區間為
的單調遞減區間為![]() ,單調遞增區間為
,單調遞增區間為![]() .
.
所以,函數![]() 的最小值為
的最小值為![]() ,
,
由題意可得![]() ,解得
,解得![]() ,
,
因此,實數![]() 的取值范圍是
的取值范圍是![]() ;
;
(2)由(1)可知,函數![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
因為![]() 為函數
為函數![]() 在
在![]() 上的零點,所以,
上的零點,所以,![]() ,①
,①
且有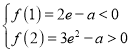 ,解得
,解得![]() .
.
![]() ,
,![]() ,
,
令![]() ,則
,則![]() ,
,
![]() ,
,![]() ,函數
,函數![]() 單調遞增,即函數
單調遞增,即函數![]() 單調遞增,
單調遞增,
而![]() ,
,![]() ,
,
所以,存在![]() ,使得
,使得![]() ,即
,即![]() ,②
,②
當![]() 時,
時,![]() ,此時,函數
,此時,函數![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,此時,函數
,此時,函數![]() 單調遞增.
單調遞增.
所以,函數![]() 在區間
在區間![]() 上的最小值為
上的最小值為![]() ,
,
由①②得![]() ,所以,
,所以,![]() ,
,
所以,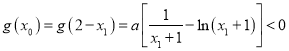 在
在![]() 上恒成立,
上恒成立,
又因為存在唯一的![]() ,使得
,使得![]() 且
且![]() ,則
,則![]() ,
,
所以![]() ,
,![]() ,解得
,解得![]() .
.
![]() ,
,![]() ,因此,實數
,因此,實數![]() 的取值范圍是
的取值范圍是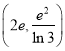 .
.


 名校聯盟快樂課堂系列答案
名校聯盟快樂課堂系列答案 黃岡創優卷系列答案
黃岡創優卷系列答案科目:高中數學 來源: 題型:
【題目】給出下列五個命題:
①函數![]() 在區間
在區間![]() 上存在零點;
上存在零點;
②要得到函數![]() 的圖象,只需將函數
的圖象,只需將函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位;
個單位;
③若![]() ,則函數
,則函數![]() 的值城為
的值城為![]() ;
;
④“![]() ”是“函數
”是“函數![]() 在定義域上是奇函數”的充分不必要條件;
在定義域上是奇函數”的充分不必要條件;
⑤已知![]() 為等差數列,若
為等差數列,若![]() ,且它的前
,且它的前![]() 項和
項和![]() 有最大值,那么當
有最大值,那么當![]() 取得最小正值時,
取得最小正值時,![]() .
.
其中正確命題的序號是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知各項均為正數的數列![]() 的前n項和為
的前n項和為![]() ,且
,且![]() ,
,![]() ,
,![]()
(1)求數列![]() 的通項公式;
的通項公式;
(2)若對![]() ,都有
,都有![]() ,求實數a的取值范圍;
,求實數a的取值范圍;
(3)當![]() 時,將數列
時,將數列![]() 中的部分項按原來的順序構成數列
中的部分項按原來的順序構成數列![]() 且
且![]() 證明:存在無數個滿足條件的無窮等比數列
證明:存在無數個滿足條件的無窮等比數列![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定數列![]() ,若滿足
,若滿足![]() (
(![]() 且
且![]() ),對于任意的
),對于任意的![]() ,都有
,都有![]() ,則稱數列
,則稱數列![]() 為“指數型數列”.
為“指數型數列”.
(1)已知數列![]() 的通項公式為
的通項公式為![]() ,試判斷數列
,試判斷數列![]() 是不是“指數型數列”;
是不是“指數型數列”;
(2)已知數列![]() 滿足
滿足![]() ,
,![]() ,證明數列
,證明數列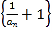 為等比數列,并判斷數列
為等比數列,并判斷數列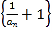 是否為“指數型數列”,若是給出證明,若不是說明理由;
是否為“指數型數列”,若是給出證明,若不是說明理由;
(3)若數列![]() 是“指數型數列”,且
是“指數型數列”,且![]() ,證明數列
,證明數列![]() 中任意三項都不能構成等差數列.
中任意三項都不能構成等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,點
,點![]() ,點
,點![]() 在圓
在圓![]() 上運動,
上運動,![]() 的垂直平分線交
的垂直平分線交![]() 于點
于點![]() .
.
(1)求證:![]() 為定值及動點
為定值及動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)不在![]() 軸上的
軸上的![]() 點為
點為![]() 上任意一點,
上任意一點,![]() 與
與![]() 關于原點
關于原點![]() 對稱,直線
對稱,直線![]() 交
交![]() 于另外一點
于另外一點![]() .求證:直線
.求證:直線![]() 與直線
與直線![]() 的斜率的乘積為定值,并求出該定值.
的斜率的乘積為定值,并求出該定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的長軸是短軸的兩倍,點
的長軸是短軸的兩倍,點![]() 在橢圓上.不過原點的直線
在橢圓上.不過原點的直線![]() 與橢圓相交于
與橢圓相交于![]() 、
、![]() 兩點,設直線
兩點,設直線![]() 、
、![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() 、
、![]() ,且
,且![]() 、
、![]() 、
、![]() 恰好構成等比數列,
恰好構成等比數列,
(1)求橢圓![]() 的方程;
的方程;
(2)試判斷![]() 是否為定值?若是,求出這個值;若不是,請說明理由?
是否為定值?若是,求出這個值;若不是,請說明理由?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】世界讀書日又稱“世界圖書日”,設立的目的是希望世界各地的人,無論你是年老還是年輕,都能享受閱讀的樂趣,都能尊重和感謝為人類文明做出巨大貢獻的文學、文化、科學、思想大師們,都能保護知識產權.某單位共有600人,其年齡與人數分布表如下:
年齡段 |
|
|
|
|
人數(單位:人) | 150 | 210 | 180 | 60 |
約定:年齡在![]() 為青年人,在
為青年人,在![]() 為中老年人.今年年初,該單位開展“每天閱讀1小時”活動,為了了解員工閱讀1小時是否與年齡相關,一個月后按照分層抽樣抽取30人進行調查.
為中老年人.今年年初,該單位開展“每天閱讀1小時”活動,為了了解員工閱讀1小時是否與年齡相關,一個月后按照分層抽樣抽取30人進行調查.
(1)抽出的青年人與中老年人數量分別為多少?并估算單位這600人的平均年齡;
(2)若所抽取出的青年人與中老年人中分別有6人和7人平均每天閱讀達1小時,其余人都沒達1小時.完成下列2×2列聯表,并回答能否由90%的把握認為年齡與閱讀達1小時有關?
閱讀達1小時 | 閱讀沒達1小時 | 總計 | |
青年 | 6 | ||
中年 | 7 | ||
總計 | 30 |
參考公式: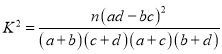
臨界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“紋樣”是中國藝術寶庫的瑰寶,“火紋”是常見的一種傳統紋樣,為了測算某火紋紋樣(如圖陰影部分所示)的面積,作一個邊長為3的正方形將其包含在內,并向該正方形內隨機投擲2000個點,己知恰有800個點落在陰影部分,據此可估計陰影部分的面積是

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com