
【題目】A,B兩組各有7位病人,他們服用某種藥物后的康復時間(單位:天)記錄如下:
A組:10,11,12,13,14,15,16
B組:12,13,15,16,17,14,a
假設所有病人的康復時間互相獨立,從A,B兩組隨機各選1人,A組選出的人記為甲,B組選出的人記為乙.
(Ⅰ)求甲的康復時間不少于14天的概率;
(Ⅱ)如果人康復時間的方差相等?(結論不要求證明)
【答案】(I)![]() ,(II)
,(II)![]() ,(III)
,(III)![]() 或18
或18
【解析】
針對甲有7種情況,康復時間不少于14天有3種情況,概率為![]() ;如果
;如果![]() ,甲、乙隨機各取一人有49種情況,用列舉法列出甲的康復時間比乙的康復時間長的情況有10種,概率為
,甲、乙隨機各取一人有49種情況,用列舉法列出甲的康復時間比乙的康復時間長的情況有10種,概率為![]() ,由于A組數據為10,11,12,13,14,15,16;B組數據調整為a,12,13,14,15,16,17,或12,13,14,15,16,17,a,由于A,B兩組病人康復時間的方差相等,即波動相同,所以
,由于A組數據為10,11,12,13,14,15,16;B組數據調整為a,12,13,14,15,16,17,或12,13,14,15,16,17,a,由于A,B兩組病人康復時間的方差相等,即波動相同,所以![]() 或18.
或18.
(1)甲有7種取法,康復時間不少于14天的有3種取法,所以概率![]() ;
;
(2)如果![]() ,從A,B兩組隨機各選1人,A組選出的人記為甲,B組選出的人記為乙共有49種取法,甲的康復時間比乙的康復時間長的列舉如下:(13,12),(14,12),(14,13),(15,12),(15,13),(15,14),(16,12)(16,13),(16,15),(16,14)有10種取法,所以概率P=
,從A,B兩組隨機各選1人,A組選出的人記為甲,B組選出的人記為乙共有49種取法,甲的康復時間比乙的康復時間長的列舉如下:(13,12),(14,12),(14,13),(15,12),(15,13),(15,14),(16,12)(16,13),(16,15),(16,14)有10種取法,所以概率P=![]()
(3)把B組數據調整為a,12,13,14,15,16,17,或12,13,14,15,16,17,a,可見當a=11或a=18時,與A組數據方差相等。
【考點精析】認真審題,首先需要了解極差、方差與標準差(標準差和方差越大,數據的離散程度越大;標準差和方程為0時,樣本各數據全相等,數據沒有離散性;方差與原始數據單位不同,解決實際問題時,多采用標準差).


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:高中數學 來源: 題型:
【題目】(2015·湖北)設函數![]() ,
,![]() 的定義域均為
的定義域均為![]() ,且
,且![]() 是奇函數,
是奇函數,![]() 是偶函數,
是偶函數,![]() ,其中e為自然對數的底數.
,其中e為自然對數的底數.
(Ⅰ)求![]() ,
,![]() 的解析式,并證明:當
的解析式,并證明:當![]() 時,
時,![]() ,
,![]() ;
;
(Ⅱ)設![]() ,
,![]() ,證明:當
,證明:當![]() 時,
時,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2015·陜西)設fn(x)是等比數列1,x,x2...,xn的各項和,其中x>0,n![]() N, ,n≥2,
N, ,n≥2,
(1)證明:函數Fn(x)=fn(x)-2在(![]() ,1)內有且僅有一個零點(記為xn),且xn=
,1)內有且僅有一個零點(記為xn),且xn=![]() +
+![]() xnn+1;
xnn+1;
(2)設有一個與上述等比數列的首項、末項、項數分別相同的等差數列,其各項和為gn(x),比較fn(x)與gn(x)的大小,并加以證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工件的三視圖如圖所示,現將該工件通過切割,加工成一個體積盡可能大的長方體新工件,并使新工件的一個面落在原工件的一個面內,則原工件材料的利用率為(材料利用率=![]() )
)
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
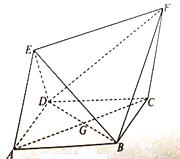
【題目】如圖,四邊形 ![]() 為菱形,四邊形
為菱形,四邊形 ![]() 為平行四邊形,設
為平行四邊形,設 ![]() 與
與 ![]() 相交于點
相交于點 ![]() ,
, ![]() .
.
(1)證明:平面 ![]() 平面
平面 ![]() ;
;
(2)若 ![]() 與平面
與平面 ![]() 所成角為60°,求二面角
所成角為60°,求二面角 ![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() 的最小正周期為4π,則( )
的最小正周期為4π,則( )
A.函數f(x)的圖象關于原點對稱
B.函數f(x)的圖象關于直線 ![]() 對稱
對稱
C.函數f(x)圖象上的所有點向右平移 ![]() 個單位長度后,所得的圖象關于原點對稱
個單位長度后,所得的圖象關于原點對稱
D.函數f(x)在區間(0,π)上單調遞增
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com