【題目】已知
為拋物線
的焦點，以為圓心作半徑為
的圓
，圓與
軸的負半軸交于點
，與拋物線
分別交于點
.
（1）若
為直角三角形，求半徑的值；
（2）判斷直線
與拋物線的位置關系，并給出證明.
【答案】(1) 
；(2) 直線
與拋物線
相切.
【解析】
(1)由對稱性可知, 
為等腰直角三角形,且
軸, 
為直徑,再根據(jù)
的橫坐標為
,代入拋物線
的方程求解縱坐標即可得半徑
.
(2)畫圖觀察可知與拋物線相切,再設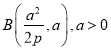
,根據(jù)圓的半徑相等求得點
坐標.再根據(jù)導數(shù)的幾何意義求解拋物線在處的切線斜率
,進而證明與直線的斜率相等即可.
(1)由拋物線與圓的對稱性可知, 點
關于
軸對稱,故
為直角.故為等腰直角三角形, 且軸,為直徑.故的橫坐標為,代入
可得
.
故.
(2)不妨設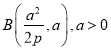.則根據(jù)拋物線的定義以及圓的半徑相等有
,故的橫坐標為
.即
.
故直線的斜率為
.
又拋物線的上半部分為函數(shù)
,故
,故在處切線的斜率為
.故直線為在處切線.
故直線與拋物線相切.
科目：高中數(shù)學 來源： 題型：
【題目】已知拋物線
的焦點為F，直線l與拋物線C交于A，B兩點，O是坐標原點.
（1）若直線l過點F且
，求直線l的方程；
（2）已知點
，若直線l不與坐標軸垂直，且
，證明：直線l過定點.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
.
(I)當a=2時,求曲線
在點
處的切線方程；
(II)設函數(shù)
,z.x.x.k討論
的單調性并判斷有無極值,有極值時求出極值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在三棱柱
中，四邊形
，
均為正方形，且
，M為
的中點，N為
的中點．
（1）求證：
平面ABC；
（2）求二面角
的正弦值；
（3）設P是棱
上一點，若直線PM與平面
所成角的正弦值為
，求
的值
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在四棱錐P-ABCD中，底面ABCD是菱形，PA=PD，∠DAB=60°.
(1)證明：AD⊥PB.
(2)若PB=
，AB=PA=2，求三棱錐P-BCD的體積。
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
的最小正周期為
，將
的圖象向左平移
個單位后，所得圖象關于原點對稱，則函數(shù)的圖象（ ）
A.關于直線
對稱B.關于直線
對稱
C.關于點(
，0)對稱D.關于點(，0)對稱
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知點
，
是橢圓
的左，右焦點，橢圓上一點
滿足
軸，
，
.
（1）求橢圓
的標準方程；
（2）過的直線
交橢圓于
兩點，當
的內切圓面積最大時，求直線的方程.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】疫情期間，為了更好地了解學生線上學習的情況，某興趣小組在網(wǎng)上隨機抽取了100名學生對其線上學習滿意情況進行調查，其中男女比例為2∶3，其中男生有24人滿意，女生有12人不滿意.
（1）完成
列聯(lián)表，并回答是否有95%把握認為“線上學習是否滿意與性別有關”
滿意 | 不滿意 | 合計 | |
男生 | |||
女生 | |||
合計 |
（2）從對線上學習滿意的學生中，利用分層抽樣抽取6名學生，再在6名學生中抽取3名，記抽到的女生人數(shù)為
，求的分布列和數(shù)學期望.
參考公式：附：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| .072 | 2.706 | 3.842 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
