
【題目】電視傳媒公司為了了解某地區電視觀眾對某類體育節目的收視情況,隨機抽取了100名觀眾進行調查,下面是根據調查結果繪制的觀眾日均收看該體育節目時間的頻率分布直方
圖:
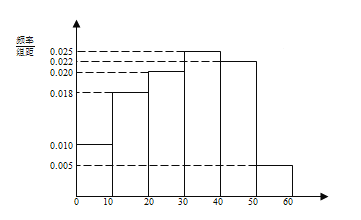
將日均收看該體育節目時間不低于40分鐘的觀眾稱為“體育迷”.
(Ⅰ)根據已知條件完成下面的![]() 列聯表,并據此資料,在犯錯誤的概率不超過
列聯表,并據此資料,在犯錯誤的概率不超過![]() 的前提下,你是否有理由認為“體育迷”與性別有關?
的前提下,你是否有理由認為“體育迷”與性別有關?
非體育迷 | 體育迷 | 合計 | |
男 | |||
女 | 10 | 55 | |
合計 |
(Ⅱ)將上述調查所得到的頻率視為概率,現在從該地區大量電視觀眾中,采用隨機抽樣方法每次抽取1名觀眾,抽取3次,記被抽取的3名觀眾中的“體育迷”人數為![]() .若每次抽取的結果是相互獨立的,求
.若每次抽取的結果是相互獨立的,求![]() 的分布列,期望
的分布列,期望![]() 和方差
和方差![]() .
.
附: 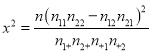
|
|
|
|
|
|
【答案】(I)沒有理由認為“體育迷”與性別有關;(II)分布列見解析, ![]() ,
, ![]() .
.
【解析】試題分析:(I)根據所給的頻率分布直方圖得出數據列出列聯表,再代入公式計算得出![]() ,與
,與![]() 比較即可得出結論;(II)由題意,用頻率代替概率可得出從觀眾中抽取一名“體育迷”的概率為
比較即可得出結論;(II)由題意,用頻率代替概率可得出從觀眾中抽取一名“體育迷”的概率為![]() ,由于
,由于![]() ,從而給出分布列,再用公式計算出期望與方差即可.
,從而給出分布列,再用公式計算出期望與方差即可.
試題解析:(Ⅰ)由頻率分布直方圖可知,在抽取的100人中,“體育迷”有25人,從而![]() 列聯表如下:
列聯表如下:
非體育迷 | 體育迷 | 合計 | |
男 | 30 | 15 | 45 |
女 | 45 | 10 | 55 |
合計 | 75 | 25 | 100 |
由![]() 列聯表中數據代入公式計算,得:
列聯表中數據代入公式計算,得:
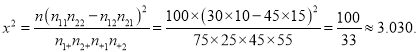
因為![]() ,所以,沒有理由認為“體育迷”與性別有關.
,所以,沒有理由認為“體育迷”與性別有關.
(Ⅱ)由頻率分布直方圖知抽到“體育迷”的頻率為![]() ,將頻率視為概率,即從觀眾中抽取一名“體育迷”的概率為
,將頻率視為概率,即從觀眾中抽取一名“體育迷”的概率為![]() ,由題意,
,由題意,
![]() ,從而
,從而![]() 的分布列為:
的分布列為:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() ,
, ![]() .
.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:
【題目】設函數![]() ,
,![]() ,
,![]() 為常數
為常數
(1)用![]() 表示
表示![]() 的最小值,求
的最小值,求![]() 的解析式
的解析式
(2)在(1)中,是否存在最小的整數![]() ,使得
,使得![]() 對于任意
對于任意![]() 均成立,若存在,求出
均成立,若存在,求出![]() 的值;若不存在,請說明理由
的值;若不存在,請說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用系統抽樣法從160名學生中抽取容量為20的樣本,將160名學生從1~160編號,按編號順序平均分成20組(1~8號,9~16號,。。。,153~160號).若第15組應抽出的號碼為116,則第一組中用抽簽方法確定的號碼是( )
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() .
.
(1)若函數![]() 在
在![]() 處有極值,求函數
處有極值,求函數![]() 的最大值;
的最大值;
(2)①是否存在實數![]() ,使得關于
,使得關于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立?若存在,求出
上恒成立?若存在,求出![]() 的取值范圍;若不存在,說明理由;
的取值范圍;若不存在,說明理由;
②證明:不等式![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
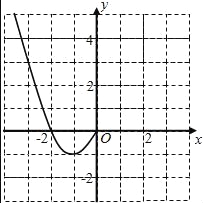
【題目】已知函數f(x)是定義在R上的偶函數,且當x≤0時,f(x)=x2+2x.
(1)現已畫出函數f(x)在y軸左側的圖象,如圖所示,請補出完整函數f(x)的圖象,并根據圖象寫出函數f(x)的增區間;
(2)寫出函數f(x)的解析式和值域.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com