
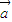 =(1,cos2θ),
=(1,cos2θ),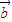 =(2,1),
=(2,1),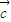 =(4sinθ,1),
=(4sinθ,1), =(
=( sinθ,1).
sinθ,1). ),求
),求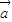 •
•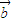 -
-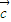 •
•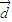 的取值范圍;
的取值范圍;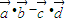 =2cos2θ,結合θ∈(0,
=2cos2θ,結合θ∈(0,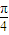 )及余弦函數的性質可求
)及余弦函數的性質可求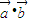 )=1+cos2θ,f(
)=1+cos2θ,f(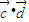 )=f(1+2sin2θ)=1-cos2θ,結合θ∈[0,π),討論cos2θ的正負即可判斷
)=f(1+2sin2θ)=1-cos2θ,結合θ∈[0,π),討論cos2θ的正負即可判斷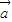 =(1,cos2θ),
=(1,cos2θ),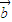 =(2,1),
=(2,1),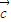 =(4sinθ,1),
=(4sinθ,1),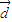 =(
=( sinθ,1)
sinθ,1)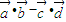 =2+cos2θ-2sin2θ-1=2cos2θ
=2+cos2θ-2sin2θ-1=2cos2θ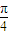 )
)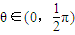
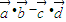 <2
<2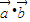 )=f(2+cos2θ)=|1+cos2θ|=1+cos2θ
)=f(2+cos2θ)=|1+cos2θ|=1+cos2θ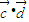 )=f(1+2sin2θ)=f(2-cos2θ)=|1-cos2θ|=1-cos2θ
)=f(1+2sin2θ)=f(2-cos2θ)=|1-cos2θ|=1-cos2θ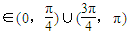 時,1-cos2θ<1+cos2θ,即f(
時,1-cos2θ<1+cos2θ,即f(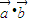 )>f(
)>f(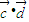 )
)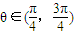 時,1-cos2θ>1+cos2θ,即f(
時,1-cos2θ>1+cos2θ,即f(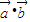 )<f(
)<f(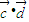 )
)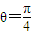 或
或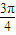 時,1-cos2θ=1+cos2θ,即f(
時,1-cos2θ=1+cos2θ,即f( )=f(
)=f( )
)

 黃岡冠軍課課練系列答案
黃岡冠軍課課練系列答案科目:高中數學 來源: 題型:
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| π |
| 3 |
| α-β |
| 2 |
查看答案和解析>>
科目:高中數學 來源:高中數學全解題庫(國標蘇教版·必修4、必修5) 蘇教版 題型:044
設向量a=(1+cosα,sinα),b=(1-cosβ,sinβ),c=(1,0),α∈![]() ,β∈(π,2π),a與c的夾角為θ1,b與c的夾角為θ2,且θ1-θ2=
,β∈(π,2π),a與c的夾角為θ1,b與c的夾角為θ2,且θ1-θ2=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:專項題 題型:解答題
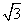 sinωx),n=(f(x),cosωx),其中ω>0,且m⊥n,又函數f(x)的圖象任意兩相鄰對稱軸間距為
sinωx),n=(f(x),cosωx),其中ω>0,且m⊥n,又函數f(x)的圖象任意兩相鄰對稱軸間距為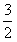 π,
π,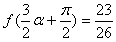 ,求
,求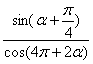 的值。
的值。查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com