
【題目】在平面直角坐標系中,圓![]() 的參數方程為
的參數方程為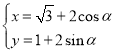 (
(![]() 為參數),以坐標原點為極點,以
為參數),以坐標原點為極點,以![]() 軸的正半軸為極軸建立極坐標系,且長度單位相同.
軸的正半軸為極軸建立極坐標系,且長度單位相同.
(1)求圓![]() 的極坐標方程;
的極坐標方程;
(2)若直線![]() :
:![]() (
(![]() 為參數)被圓
為參數)被圓![]() 截得的弦長為2,求直線
截得的弦長為2,求直線![]() 的傾斜角.
的傾斜角.
 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:
【題目】2020年是我國全面建成小康社會和“十三五”規劃收官之年,也是佛山在經濟總量超萬億元新起點上開啟發展新征程的重要歷史節點.作為制造業城市,佛山一直堅持把創新擺在制造業發展全局的前置位置和核心位置,聚焦打造成為面向全球的國家制造業創新中心,走“世界科技+佛山智造+全球市場”的創新發展之路.在推動制造業高質量發展的大環境下,佛山市某工廠統籌各類資源,進行了積極的改革探索.下表是該工廠每月生產的一種核心產品的產量![]() (件)與相應的生產總成本
(件)與相應的生產總成本![]() (萬元)的四組對照數據.
(萬元)的四組對照數據.
| 5 | 7 | 9 | 11 |
| 200 | 298 | 431 | 609 |
工廠研究人員建立了![]() 與
與![]() 的兩種回歸模型,利用計算機算得近似結果如下:
的兩種回歸模型,利用計算機算得近似結果如下:
模型①:![]() ;
;
模型②:![]() .
.
其中模型①的殘差(實際值預報值)圖如圖所示:
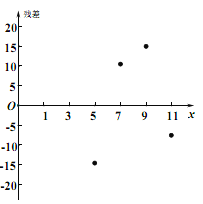
(1)根據殘差分析,判斷哪一個更適宜作為![]() 關于
關于![]() 的回歸方程?并說明理由;
的回歸方程?并說明理由;
(2)市場前景風云變幻,研究人員統計了20個月的產品銷售單價,得到頻數分布表如下:
銷售單價分組(萬元) |
|
|
|
頻數 | 10 | 6 | 4 |
若以這20個月銷售單價的平均值定為今后的銷售單價(同一組中的數據用該組區間的中點值作代表),結合你對(1)的判斷,當月產量為12件時,預測當月的利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩個班級(各40名學生)進行一門考試,為易于統計分析,將甲、乙兩個班學生的成績分成如下四組:![]() ,
,![]() ,
,![]() ,
,![]() ,并分別繪制了如下的頻率分布直方圖:
,并分別繪制了如下的頻率分布直方圖:
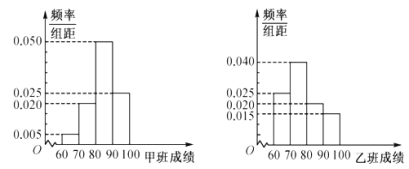
規定:成績不低于90分的為優秀,低于90分的為不優秀.
(1)根據這次抽查的數據,填寫下面的![]() 列聯表:
列聯表:
優秀 | 不優秀 | 合計 | |
甲班 | |||
乙班 | |||
合計 |
(2)根據(1)中的列聯表,能否有![]() 的把握認為成績是否優秀與班級有關?
的把握認為成績是否優秀與班級有關?
附:臨界值參考表與參考公式
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(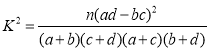 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業新研發了一種產品,產品的成本由原料成本及非原料成本組成.每件產品的非原料成本![]() (元)與生產該產品的數量
(元)與生產該產品的數量![]() (千件)有關,經統計得到如下數據:
(千件)有關,經統計得到如下數據:
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y | 112 | 61 | 44.5 | 35 | 30.5 | 28 | 25 | 24 |
根據以上數據,繪制了散點圖.觀察散點圖,兩個變量不具有線性相關關系,現考慮用反比例函數模型![]() 和指數函數模型
和指數函數模型![]() 分別對兩個變量的關系進行擬合,已求得:用指數函數模型擬合的回歸方程為
分別對兩個變量的關系進行擬合,已求得:用指數函數模型擬合的回歸方程為![]() ,
,![]() 與
與![]() 的相關系數
的相關系數![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(其中
,(其中![]() );
);
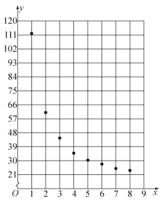
(1)用反比例函數模型求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(2)用相關系數判斷上述兩個模型哪一個擬合效果更好(精確到0.01),并用其估計產量為10千件時每件產品的非原料成本.
參考數據:![]() ,
,![]()
參考公式:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: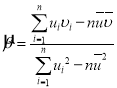 ,
,![]() ,相關系數
,相關系數 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的多面體中,AD⊥平面PDC,四邊形ABCD為平行四邊形,E為AD的中點,F為線段PB上的一點,∠CDP=120°,AD=3,AP=5,![]() .
.
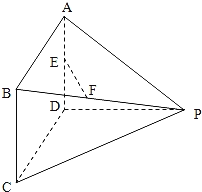
(Ⅰ)試確定點F的位置,使得直線EF∥平面PDC;
(Ⅱ)若PB=3BF,求直線AF與平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,過點![]() 的直線l與拋物線
的直線l與拋物線![]() 交于A,B兩點,以AB為直徑作圓,記為
交于A,B兩點,以AB為直徑作圓,記為![]() ,
,![]() 與拋物線C的準線始終相切.
與拋物線C的準線始終相切.
(1)求拋物線C的方程;
(2)過圓心M作x軸垂線與拋物線相交于點N,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校高三年級為了解學生在家參加線上教學的學習情況,對高三年級進行了網上數學測試,他們的成績在80分到150分之間,根據統計數據得到如下頻率分布直方圖:
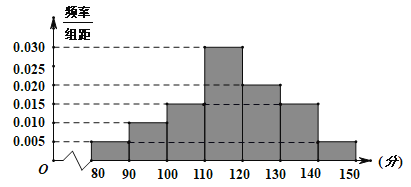
若成績在區![]() 左側,認為該學生屬于“網課潛能生”,成績在區間
左側,認為該學生屬于“網課潛能生”,成績在區間![]() 之間,認為該學生屬于“網課中等生”,成績在區間
之間,認為該學生屬于“網課中等生”,成績在區間![]() 右側,認為該學生屬于“網課優等生”.
右側,認為該學生屬于“網課優等生”.
(1)若小明的測試成績為100分,請判斷小明是否屬于“網課潛能生”,并說明理由:(參考數據:計算得![]() )
)
(2)該校利用分層抽樣的方法從樣本的![]() ,
,![]() 兩組中抽出6人,進行教學反饋,并從這6人中再抽取2人,贈送一份學習資料,求獲贈學習資料的2人中恰有1人成績超過90分的概率.
兩組中抽出6人,進行教學反饋,并從這6人中再抽取2人,贈送一份學習資料,求獲贈學習資料的2人中恰有1人成績超過90分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() ,
,![]() 分別是其左、右焦點,過
分別是其左、右焦點,過![]() 的直線l與橢圓C交于A,B兩點,且橢圓C的離心率為
的直線l與橢圓C交于A,B兩點,且橢圓C的離心率為![]() ,
,![]() 的內切圓面積為
的內切圓面積為![]() ,
,![]() .
.
(I)求橢圓C的方程;
(II)若![]() 時,求直線l的方程
時,求直線l的方程
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com