
 -4a2-b2≤t-
-4a2-b2≤t- 恒成立,則實數t的取值范圍是 .
恒成立,則實數t的取值范圍是 . 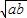 -4a2-b2≤t-
-4a2-b2≤t- 恒成立?t≥2
恒成立?t≥2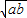 -(1-4ab)+
-(1-4ab)+ =4ab+2
=4ab+2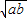 -
- =4
=4 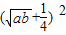 -
- 恒成立,故t需大于或等于4
恒成立,故t需大于或等于4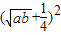 -
- 的最大值,由基本不等式可求得
的最大值,由基本不等式可求得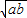 的最大值,從而得到4
的最大值,從而得到4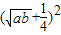 -
- 的最大值,問題解決了.
的最大值,問題解決了.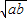 -4a2-b2≤t-
-4a2-b2≤t- 恒成立可轉化為:t≥2
恒成立可轉化為:t≥2 -(1-4ab)+
-(1-4ab)+ 恒成立;
恒成立;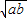 -(1-4ab)+
-(1-4ab)+ =4ab+2
=4ab+2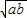 -
- =4
=4 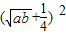 -
- ,
,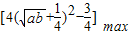 (a>0,b>0,2a+b=1),
(a>0,b>0,2a+b=1),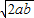 ,故
,故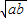 ≤
≤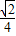 (當且僅當2a=b=
(當且僅當2a=b= 時取“=”),
時取“=”),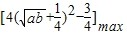 =4
=4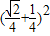 -
- =
=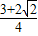 -
- =
=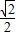 .
.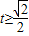 .
.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com