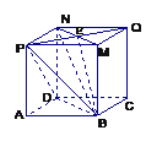
【題目】如圖（1）是一正方體的表面展開圖，MN和PB是兩條面對角線，請在圖（2）的正方體中將MN和PB畫出來，并就這個正方體解決下面問題。
（1）求證：MN∥平面PBD；
（2）求證：
平面
；
（3）求PB和平面NMB所成的角的大小．
【答案】（1）見解析；（2）見解析；（3）
【解析】
由展開圖還原出原圖形，由正方體可證MN//DB,進一步證明MN∥平面PBD。通過證明
平面
,可證
，同理可得
，所以
面PDB。連結BE,則
為PB和平面NMB所成的角。
MN和PB的位置如右圖示：
（1）∵ND∥MB 且ND＝MB，∴四邊形NDBM為平行四邊形
∴MN//DB
∵
平面PDB,
平面PDB
∴MN∥平面PBD
（2）∵
平面ABCD，
平面
，∴
又∵
∴平面,
面 ∴,同理可得,∵
∴面PDB
（3）連結PQ交MN于點E,
∵
,
∴
平面
連結BE,則為PB和平面NMB所成的角
在直角三角形PEB中∵
∴=30°.
即PB和平面NMB所成的角為30°
舉一反三期末百分沖刺卷系列答案科目：高中數學 來源： 題型：
【題目】在去年的足球甲
聯賽上，一隊每場比賽平均失球數是1.5，全年比賽失球個數的標準差為1.1；二隊每場比賽平均失球數是2.1，全年失球個數的標準差是0.4，你認為下列說法中正確的個數有（ ）
①平均來說一隊比二隊防守技術好；②二隊比一隊防守技術水平更穩定；③一隊防守有時表現很差，有時表現又非常好；④二隊很少不失球.
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法：
①將一組數據中的每個數據都加上或減去同一個常數后，方差恒不變；
②設有一個回歸方程
，變量x增加一個單位時，y平均增加5個單位；
③線性回歸直線
必過
；
④曲線上的點與該點的坐標之間具有相關關系；
⑤在一個2×2列聯表中，由計算得K2＝13.079.則其兩個變量間有關系的可能性是90%.
其中錯誤的個數是( )
A. 1 B. 2
C. 3 D. 4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知某射擊運動員，每次擊中目標的概率都是
.現采用隨機模擬的方法估計該運動員射擊
次至少擊中
次的概率：先由計算器算出
到
之間取整數值的隨機數，指定，
表示沒有擊中目標，
，，，
，
，
，
，表示擊中目標；因為射擊次，故以每個隨機數為一組，代表射擊次的結果.經隨機模擬產生了如下
組隨機數：
據此估計，該射擊運動員射擊次至少擊中次的概率為（ ）
A. 
B. 
C. D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在四棱錐
中，
平面
，
是正三角形，
與
的交點
恰好是中點，又
，
，點
在線段
上，且
．
（
）求證：
．
（
）求證：
平面
．
（
）設平面
平面
，試問：直線
是否與直線
平行，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
