
如圖,在三棱錐P-ABC中,AB⊥BC,AB=BC=kPA,點O、D分別是AC、PC的中點,OP⊥底面ABC.
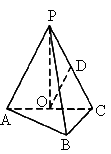
(1)求證:OD∥平面PAB;
(2)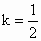 時,求直線PA與平面PBC所成的角的正弦值;
時,求直線PA與平面PBC所成的角的正弦值;
(3)當k取何值時,O在平面PBC內的射影恰好為△PBC的重心?
|
(1) 證明:∵O、D分別為AC、PC的中點,∴OD∥PA.又∵ PA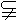 平面PAB 平面PAB
∴ OD∥平面PAB(2) 解:∵AB⊥BC,OA=OC,∴ OA=OA=OC又∵ OP⊥平面ABC,∴ PA=PB=PC.取 BC中點E,連結PE.則BC⊥平面POE.作 OF⊥PE于F,連結DF,則OF⊥平面PBC.∴∠ ODF是OD與平面PBC所成的角.又OD∥PA,∴ PA與平面PBC所成角的大小等于∠ODF.在Rt△ODF中,
(3) 解由(2)知,OF⊥平面PBC,∴ F是O在平面PBC內的射影.∵ D是PC的中點,若點F是△PBC的重心,則B、F、D三點共線.∴直線 OB在平面PBC內的射影為直線BD.∵ OD⊥PC,∴PC⊥BD.∴ PB=BC,即k=1.反之,當 k=1時,三棱錐O-PBC為正三棱錐,∴ O在平面PBC內的射影為△PBC的重心. |


科目:高中數學 來源: 題型:
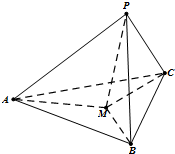 如圖,在三棱錐P-ABC中,PA、PB、PC兩兩垂直,且PA=3.PB=2,PC=1.設M是底面ABC內一點,定義f(M)=(m,n,p),其中m、n、p分別是三棱錐M-PAB、三棱錐M-PBC、三棱錐M-PCA的體積.若f(M)=(
如圖,在三棱錐P-ABC中,PA、PB、PC兩兩垂直,且PA=3.PB=2,PC=1.設M是底面ABC內一點,定義f(M)=(m,n,p),其中m、n、p分別是三棱錐M-PAB、三棱錐M-PBC、三棱錐M-PCA的體積.若f(M)=(| 1 |
| 2 |
| 1 |
| x |
| a |
| y |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在三棱錐P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,則當△AEF的面積最大時,tanθ的值為( )
如圖,在三棱錐P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,則當△AEF的面積最大時,tanθ的值為( )查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在三棱錐P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分別為AB、AC中點.
如圖,在三棱錐P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分別為AB、AC中點.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在三棱錐P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一繩子從A點繞三棱錐側面一圈回到點A的最短距離是
如圖,在三棱錐P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一繩子從A點繞三棱錐側面一圈回到點A的最短距離是| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在三棱錐P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,點D,E分別在棱
如圖,在三棱錐P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,點D,E分別在棱查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com