Question

【題目】萬眾矚目的第14屆全國冬季運動運會（簡稱“十四冬”）于2020年2月16日在呼倫貝爾市盛大開幕，期間正值我市學校放寒假，寒假結束后，某校工會對全校100名教職工在“十四冬”期間每天收看比賽轉播的時間作了一次調查，得到如圖頻數分布直方圖：

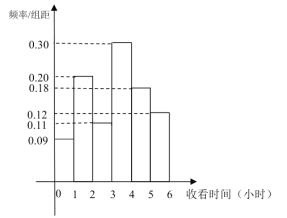
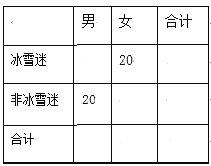
（1）若將每天收看比賽轉播時間不低于3小時的教職工定義為“冰雪迷”，否則定義為“非冰雪迷”，請根據頻率分布直方圖補全列聯表；并判斷能否有的把握認為該校教職工是否為“冰雪迷”與“性別”有關；

（2）在全校“冰雪迷”中按性別分層抽樣抽取6名，再從這6名“冰雪迷”中選取2名作冰雪運動知識講座.記其中女職工的人數為，求的分布列與數學期望.

附表及公式：

	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	2.072	2.706	3.841	5.024	6.635	7.879	10.828

，

Answer 1

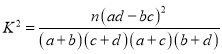【答案】（1）列聯表見解析，有把握；（2）分布列見解析，.

【解析】

（1）根據頻率分布直方圖補全列聯表，求出，從而有的把握認為該校教職工是否為“冰雪迷”與“性別”有關．

（2）在全校“冰雪迷”中按性別分層抽樣抽取6名，則抽中男教工：人，抽中女教工：人，從這6名“冰雪迷”中選取2名作冰雪運動知識講座．記其中女職工的人數為，則的可能取值為0，1，2，分別求出相應的概率，由此能求出的分布列和數學期望．

解：（1）由題意得下表：

	男	女	合計
冰雪迷	40	20	60
非冰雪迷	20	20	40
合計	60	40	100

的觀測值為

所以有的把握認為該校教職工是“冰雪迷”與“性別”有關.

（2）由題意知抽取的6名“冰雪迷”中有4名男職工，2名女職工，

所以的可能取值為0，1，2.

且，，，

所以的分布列為

	0	1	2