
【題目】已知函數![]() .
.
(1)若函數![]() 在
在![]() 處的切線方程
處的切線方程![]() ,求實數a,b的值;
,求實數a,b的值;
(2)若函數![]() 在
在![]() 和
和![]() 兩處得極值,求實數a的取值范圍;
兩處得極值,求實數a的取值范圍;
(3)在(2)的條件下,若![]() .求實數a的取值范圍.
.求實數a的取值范圍.
【答案】(1)![]() ,
,![]() .(2)
.(2)![]() (3)
(3)![]()
【解析】
(1)對函數進行求導,將![]() 代入,可以求得實數
代入,可以求得實數![]() 的值;
的值;
(2)對函數的導數再進行求導,對![]() 進行分情況討論,在不同情況下,函數
進行分情況討論,在不同情況下,函數![]() 都有兩個極值,從而求出實數
都有兩個極值,從而求出實數![]() 的取值范圍;
的取值范圍;
(3) 由題意得: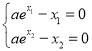 ,即
,即![]() ,令
,令![]() 則
則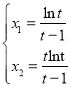 ,令
,令![]() ,求導可得
,求導可得![]() 在
在![]() 上單調遞減,則
上單調遞減,則![]() ,即
,即![]() .
.
由于![]() ,構造函數
,構造函數![]() ,求導可知
,求導可知![]() 在
在![]() 上單調遞減,計算即可得出結果.
上單調遞減,計算即可得出結果.
解:(1)![]()
由題意得:![]() ,即
,即![]() ,
,
![]() ,即
,即![]() ,所以
,所以![]() ,
,![]() .
.
(2)由題意知:![]() 有兩個零點
有兩個零點![]() ,
,![]() ,
,
令![]() ,而
,而![]() ,
,
①當![]() 時,
時,![]() 恒成立,
恒成立,
所以![]() 單調遞減,此時
單調遞減,此時![]() 至多
至多![]() 個零點(舍).
個零點(舍).
②當![]() 時,令
時,令![]() ,解得:
,解得:![]() ,
,
![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
所以![]() .
.
因為![]() 有兩個零點,所以
有兩個零點,所以![]() ,
,
解得:![]() .
.
因為![]() ,
,![]() ,且
,且![]() ,
,
而![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() 在
在![]() 上有1個零點.
上有1個零點.
又因為![]() (易證
(易證![]() ),
),
則![]() 且
且![]() ,
,
而![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() 在
在![]() 上有1個零點,
上有1個零點,
綜上:![]() .
.
(3)由題意得: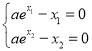 ,即
,即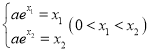 ,
,
所以![]() ,令
,令![]() ,
,
即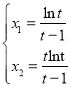 ,
,
令![]() ,
,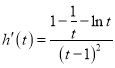 ,
,
令![]() .而
.而![]() ,
,
所以![]() 在
在![]() 上單調遞減,即
上單調遞減,即![]() ,
,
所以![]() 在
在![]() 上單調遞減,即
上單調遞減,即![]() .
.
因為![]() ,
,![]() ,
,
令![]() ,而
,而![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上單調遞減,又
上單調遞減,又![]() ,
,
所以![]() .
.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]()
![]() 的左右焦點分別為的
的左右焦點分別為的![]() 、
、![]() ,離心率為
,離心率為![]() ;過拋物線
;過拋物線![]() 焦點
焦點![]() 的直線交拋物線于
的直線交拋物線于![]() 、
、![]() 兩點,當
兩點,當![]() 時,
時, ![]() 點在
點在![]() 軸上的射影為
軸上的射影為![]() 。連結
。連結![]() 并延長分別交
并延長分別交![]() 于
于![]() 、
、![]() 兩點,連接
兩點,連接![]() ;
; ![]() 與
與![]() 的面積分別記為
的面積分別記為![]() ,
, ![]() ,設
,設![]() .
.
(Ⅰ)求橢圓![]() 和拋物線
和拋物線![]() 的方程;
的方程;
(Ⅱ)求![]() 的取值范圍.
的取值范圍.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,
,![]() ).
).
(1)當![]() 時,若函數
時,若函數![]() 在
在![]() 上有兩個零點,求
上有兩個零點,求![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,是否存在
時,是否存在![]() ,使得不等式
,使得不等式![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值集合;若不存在,請說明理由.
的取值集合;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著經濟的快速增長、規模的迅速擴張以及人民生活水平的逐漸提高,日益劇增的垃圾給城市的綠色發展帶來了巨大的壓力.相關部門在有5萬居民的光明社區采用分層抽樣方法得到年內家庭人均![]() 與人均垃圾清運量的統計數據如下表:
與人均垃圾清運量的統計數據如下表:
人均 | 3 | 6 | 9 | 12 | 15 |
人均垃圾清運量 | 0.13 | 0.23 | 0.31 | 0.41 | 0.52 |
(1)已知變量![]() 與
與![]() 之間存在線性相關關系,求出其回歸直線方程;
之間存在線性相關關系,求出其回歸直線方程;
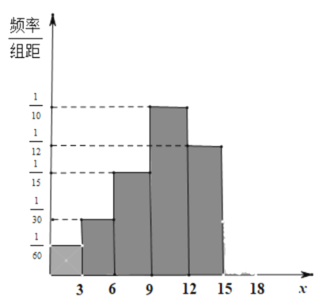
(2)隨著垃圾分類的推進,燃燒垃圾發電的熱值大幅上升,平均每噸垃圾可折算成上網電量200千瓦時,如圖是光明社區年內家庭人均![]() 的頻率分布直方圖,請補全
的頻率分布直方圖,請補全![]() 的缺失部分,并利用(1)的結果,估計整個光明社區年內垃圾可折算成的總上網電量.
的缺失部分,并利用(1)的結果,估計整個光明社區年內垃圾可折算成的總上網電量.
參考公式]回歸方程![]() ,
,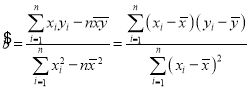
查看答案和解析>>
科目:高中數學 來源: 題型:
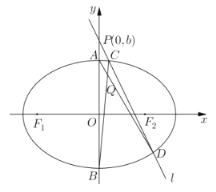
【題目】在平面直角坐標系中,A、B分別為橢圓![]() 的上、下頂點,若動直線l過點
的上、下頂點,若動直線l過點![]() ,且與橢圓
,且與橢圓![]() 相交于C、D兩個不同點(直線l與y軸不重合,且C、D兩點在y軸右側,C在D的上方),直線AD與BC相交于點Q.
相交于C、D兩個不同點(直線l與y軸不重合,且C、D兩點在y軸右側,C在D的上方),直線AD與BC相交于點Q.
(1)設![]() 的兩焦點為
的兩焦點為![]() 、
、![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,求點Q的橫坐標;
,求點Q的橫坐標;
(3)是否存在這樣的點P,使得點Q的縱坐標恒為![]() ?若存在,求出點P的坐標,若不存在,請說明理由.
?若存在,求出點P的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知O為坐標原點,![]() ,
,![]() ,直線AG,BG相交于點G,且它們的斜率之積為
,直線AG,BG相交于點G,且它們的斜率之積為![]() .記點G的軌跡為曲線C.
.記點G的軌跡為曲線C.
(1)若射線![]() 與曲線C交于點D,且E為曲線C的最高點,證明:
與曲線C交于點D,且E為曲線C的最高點,證明:![]() .
.
(2)直線![]() 與曲線C交于M,N兩點,直線AM,AN與y軸分別交于P,Q兩點.試問在x軸上是否存在定點T,使得以PQ為直徑的圓恒過點T?若存在,求出T的坐標;若不存在,請說明理由.
與曲線C交于M,N兩點,直線AM,AN與y軸分別交于P,Q兩點.試問在x軸上是否存在定點T,使得以PQ為直徑的圓恒過點T?若存在,求出T的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com