
【題目】如圖,橢圓![]()
![]() 的左右焦點分別為的
的左右焦點分別為的![]() 、
、![]() ,離心率為
,離心率為![]() ;過拋物線
;過拋物線![]() 焦點
焦點![]() 的直線交拋物線于
的直線交拋物線于![]() 、
、![]() 兩點,當
兩點,當![]() 時,
時, ![]() 點在
點在![]() 軸上的射影為
軸上的射影為![]() 。連結
。連結![]() 并延長分別交
并延長分別交![]() 于
于![]() 、
、![]() 兩點,連接
兩點,連接![]() ;
; ![]() 與
與![]() 的面積分別記為
的面積分別記為![]() ,
, ![]() ,設
,設![]() .
.
(Ⅰ)求橢圓![]() 和拋物線
和拋物線![]() 的方程;
的方程;
(Ⅱ)求![]() 的取值范圍.
的取值范圍.

【答案】(1) ![]() ,
,![]() ;(2)
;(2) ![]() .
.
【解析】試題分析:(Ⅰ )由題意得得![]() ,根據點M在拋物線上得
,根據點M在拋物線上得![]() ,又由
,又由![]() ,得
,得 ![]() ,可得
,可得![]() ,解得
,解得![]() ,從而得
,從而得![]() ,可得曲線方程。(Ⅱ )設
,可得曲線方程。(Ⅱ )設![]() ,
, ![]() ,分析可得
,分析可得![]() ,先設出直線
,先設出直線![]() 的方程為
的方程為![]()
![]() ,由
,由![]() ,解得
,解得![]() ,從而可求得
,從而可求得![]() ,同理可得
,同理可得![]() ,故可將
,故可將![]() 化為m的代數式,用基本不等式求解可得結果。
化為m的代數式,用基本不等式求解可得結果。
試題解析:
(Ⅰ)由拋物線定義可得![]() ,
,
∵點M在拋物線![]() 上,
上,
∴![]() ,即
,即![]() ①
①
又由![]() ,得
,得 ![]()
將上式代入①,得![]()
解得![]()
∴![]()
![]() ,
,
所以曲線![]() 的方程為
的方程為![]() ,曲線
,曲線![]() 的方程為
的方程為![]() 。
。
(Ⅱ)設直線![]() 的方程為
的方程為![]() ,
,
由![]() 消去y整理得
消去y整理得![]() ,
,
設![]() ,
, ![]() .
.
則![]() ,
,
設![]() ,
, ![]() ,
,
則![]() ,
,
所以![]() , ②
, ②
設直線![]() 的方程為
的方程為![]()
![]() ,
,
由![]() ,解得
,解得![]() ,
,
所以![]() ,
,
由②可知,用![]() 代替
代替![]() ,
,
可得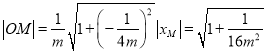 ,
,
由 ,解得
,解得![]() ,
,
所以 ,
,
用![]() 代替
代替![]() ,可得
,可得
所以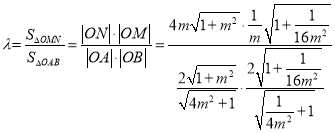
![]()
![]() ,當且僅當
,當且僅當![]() 時等號成立。
時等號成立。
所以![]() 的取值范圍為
的取值范圍為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】2017年9月16日05時,第19號臺風“杜蘇芮”的中心位于甲地,它以每小時30千米的速度向西偏北![]() 的方向移動,距臺風中心
的方向移動,距臺風中心![]() 千米以內的地區都將受到影響,若16日08時到17日08時,距甲地正西方向900千米的乙地恰好受臺風影響,則
千米以內的地區都將受到影響,若16日08時到17日08時,距甲地正西方向900千米的乙地恰好受臺風影響,則![]() 和
和![]() 的值分別為(附:
的值分別為(附: ![]() )( )
)( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經市場調查,某城市的一種小商品在過去的近20天內的銷售量(件)與價格(元)均為時間t(天)的函數,且銷售量近似滿足g(t)=80﹣2t(件),價格近似滿足于  (元).
(元).
(1)試寫出該種商品的日銷售額y與時間t(0≤t≤20)的函數表達式;
(2)求該種商品的日銷售額y的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的離心率為
的離心率為![]() ,頂點為
,頂點為![]() ,且
,且![]() .
.

(1)求橢圓![]() 的方程;
的方程;
(2)![]() 是橢圓
是橢圓![]() 上除頂點外的任意點,直線
上除頂點外的任意點,直線![]() 交
交![]() 軸于點
軸于點![]() ,直線
,直線![]() 交
交![]() 于點
于點![]() .設
.設![]() 的斜率為
的斜率為![]() ,
, ![]() 的斜率為
的斜率為![]() ,試問
,試問![]() 是否為定值?并說明理由.
是否為定值?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面內動點P(x,y)與兩定點A(-2, 0), B(2,0)連線的斜率之積等于![]() ,若點P的軌跡為曲線E,過點Q
,若點P的軌跡為曲線E,過點Q![]() 作斜率不為零的直線
作斜率不為零的直線![]() 交曲線E于點
交曲線E于點![]() .
.
(I)求曲線E的方程;
(II)求證: ![]() ;
;
(III)求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數t滿足f(0)=f(2)=2,f(1)=1.
(1)求函數f(x)的解析式;
(2)當x∈[﹣1,2]時,求y=f(x)的值域;
(3)設h(x)=f(x)﹣mx在[1,3]上是單調函數,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
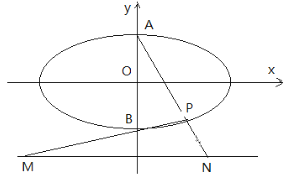
【題目】如圖橢圓![]() 的上下頂點為A、B,直線
的上下頂點為A、B,直線![]() :
: ![]() ,點P是橢圓上異于點A、B的任意一點,連結AP并延長交直線
,點P是橢圓上異于點A、B的任意一點,連結AP并延長交直線![]() 于點N,連結BP并延長交直線
于點N,連結BP并延長交直線![]() 于點M,設AP、BP所在直線的斜率分別為
于點M,設AP、BP所在直線的斜率分別為![]() ,若橢圓的離心率為
,若橢圓的離心率為![]() ,且過點
,且過點![]() ,(1)求
,(1)求![]() 的值,并求
的值,并求![]() 最小值;(2)隨著點P的變化,以MN為直徑的圓是否恒過定點,若過定點,求出該定點坐標;若不過定點,請說明理由。
最小值;(2)隨著點P的變化,以MN為直徑的圓是否恒過定點,若過定點,求出該定點坐標;若不過定點,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】傳承傳統文化再掀熱潮,央視科教頻道以詩詞知識競賽為主的《中國詩詞大會》火爆熒屏。將中學組和大學組的參賽選手按成績分為優秀、良好、一般三個等級,隨機從中抽取了100名選手進行調查,下面是根據調查結果繪制的選手等級人數的條形圖.
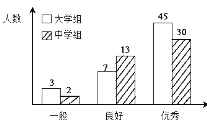
(Ⅰ)若將一般等級和良好等級合稱為合格等級,根據已知條件完成下面的2×2列聯表,并據此資料你是否有95﹪的把握認為選手成績“優秀”與文化程度有關?
優秀 | 合格 | 合計 | |
大學組 | |||
中學組 | |||
合計 |
注: 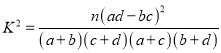 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0. 005 |
| 2.706 | 3.841 | 7.879 |
(Ⅱ)若江西參賽選手共80人,用頻率估計概率,試估計其中優秀等級的選手人數;
(Ⅲ)如果在優秀等級的選手中取4名,在良好等級的選手中取2名,再從這6人中任選3人組成一個比賽團隊,求所選團隊中的有2名選手的等級為優秀的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com