
【題目】在平面直角坐標系![]() 中,已知圓
中,已知圓![]() 的圓心在
的圓心在![]() 軸右側,原點
軸右側,原點![]() 和點
和點![]() 都在圓
都在圓![]() 上,且圓
上,且圓![]() 在
在![]() 軸上截得的線段長度為3.
軸上截得的線段長度為3.
(1)求圓![]() 的方程;
的方程;
(2)若![]() ,
,![]() 為圓
為圓![]() 上兩點,若四邊形
上兩點,若四邊形![]() 的對角線
的對角線![]() 的方程為
的方程為![]() ,求四邊形
,求四邊形![]() 面積的最大值;
面積的最大值;
(3)過點![]() 作兩條相異直線分別與圓
作兩條相異直線分別與圓![]() 相交于
相交于![]() ,
,![]() 兩點,若直線
兩點,若直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,且
,且![]() ,試判斷直線
,試判斷直線![]() 的斜率是否為定值,并說明理由.
的斜率是否為定值,并說明理由.
【答案】(1)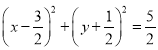 ;(2)
;(2)![]() ;(3)是定值,理由詳見解析.
;(3)是定值,理由詳見解析.
【解析】
(1)設出圓的一般方程代入三點坐標,可得圓方程,配方后可得圓標準方程;
(2)求出圓心到直線![]() 的距離
的距離![]() ,由勾股定理求得弦長
,由勾股定理求得弦長![]() ,由
,由![]() 小于半徑得
小于半徑得![]() 的一個范圍,由
的一個范圍,由![]() 在直線
在直線![]() 兩側又得一個范圍,綜合即得
兩側又得一個范圍,綜合即得![]() 的取值范圍,然后分別求出
的取值范圍,然后分別求出![]() 到直線
到直線![]() 的距離,得四邊形面積,可得最大值.
的距離,得四邊形面積,可得最大值.
(3)設![]() ,與圓方程聯立,由于直線與圓的一個交點為
,與圓方程聯立,由于直線與圓的一個交點為![]() ,因此由韋達定理可求得
,因此由韋達定理可求得![]() 點坐標,同理可得
點坐標,同理可得![]() 點坐標,計算
點坐標,計算![]() 即得.
即得.
(1)由已知圓![]() 過
過![]() ,
,![]() ,
,![]() 三點
三點
設圓![]() 方程為
方程為![]() ,則有
,則有
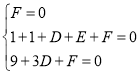 ,解得
,解得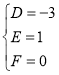
所以圓![]() 方程為
方程為![]() ,即
,即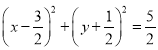 .
.
(2)由(1)可知![]() ,半徑
,半徑![]() ,
,
則![]() 到
到![]() 距離
距離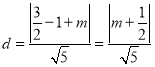 ,
,
所以![]() ,
,
當且僅當![]() 時取等號,
時取等號,
由![]() 解得
解得![]() ;
;
由![]() ,
,![]() 在
在![]() 兩側,
兩側,![]() ,
,![]() ,
,
所以![]() ,
,
![]() 到
到![]() 距離
距離![]() ,
,![]() 到
到![]() 距離
距離![]() ,
,
所以四邊形![]() 的面積
的面積![]() ,
,
所以![]() 時,四邊形
時,四邊形![]() 面積最大為
面積最大為![]() .
.
(3)由題意可設![]()
由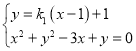 可得
可得![]() ,
,
設![]() ,則
,則![]() ,
,
所以![]() ,
,![]() ,
,
同理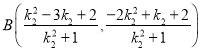 ,
,
因為![]() ,所以
,所以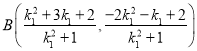 ,
,
所以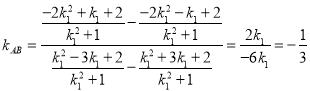 為定值.
為定值.


科目:高中數學 來源: 題型:
【題目】祖暅是我國南北朝時期杰出的數學家和天文學家祖沖之的兒子,他提出了一條原理:“冪勢既同冪,則積不容異”.這里的“冪”指水平截面的面積,“勢”指高.這句話的意思是:兩個等高的幾何體若在所有等高處的水平截面的面積相等,則這兩個幾何體體積相等.一般大型熱電廠的冷卻塔大都采用雙曲線型.設某雙曲線型冷卻塔是曲線![]()
![]() 與直線
與直線![]() ,
, ![]() 和
和![]() 所圍成的平面圖形繞
所圍成的平面圖形繞![]() 軸旋轉一周所得,如圖所示.試應用祖暅原理類比求球體體積公式的方法,求出此冷卻塔的體積為_______.
軸旋轉一周所得,如圖所示.試應用祖暅原理類比求球體體積公式的方法,求出此冷卻塔的體積為_______.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】總體由編號為01,02,…,19,20的20個個體組成,利用下面的隨機數表選取6個個體,選取方法從隨機數表第1行的第5列和第6列數字開始由左到右依次選取兩個數字,則選出來的第6個個體的編號為( )
7816 6572 0802 6314 0702 4369 9728 0198 |
3204 9234 4935 8200 3623 4869 6938 7481 |
A.07B.04C.02D.01
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型超市在2018年元旦舉辦了一次抽獎活動,抽獎箱里放有3個紅球,3個黃球和1個藍球(這些小球除顏色外大小形狀完全相同),從中隨機一次性取3個小球,每位顧客每次抽完獎后將球放回抽獎箱.活動另附說明如下:
①凡購物滿100(含100)元者,憑購物打印憑條可獲得一次抽獎機會;
②凡購物滿188(含188)元者,憑購物打印憑條可獲得兩次抽獎機會;
③若取得的3個小球只有1種顏色,則該顧客中得一等獎,獎金是一個10元的紅包;
④若取得的3個小球有3種顏色,則該顧客中得二等獎,獎金是一個5元的紅包;
⑤若取得的3個小球只有2種顏色,則該顧客中得三等獎,獎金是一個2元的紅包.
抽獎活動的組織者記錄了該超市前20位顧客的購物消費數據(單位:元),繪制得到如圖所示的莖葉圖.

(1)求這20位顧客中獎得抽獎機會的顧客的購物消費數據的中位數與平均數(結果精確到整數部分);
(2)記一次抽獎獲得的紅包獎金數(單位:元)為![]() ,求
,求![]() 的分布列及數學期望,并計算這20位顧客(假定每位獲得抽獎機會的顧客都會去抽獎)在抽獎中獲得紅包的總獎金數的平均值.
的分布列及數學期望,并計算這20位顧客(假定每位獲得抽獎機會的顧客都會去抽獎)在抽獎中獲得紅包的總獎金數的平均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型超市在2018年元旦舉辦了一次抽獎活動,抽獎箱里放有3個紅球,3個黃球和1個藍球(這些小球除顏色外大小形狀完全相同),從中隨機一次性取3個小球,每位顧客每次抽完獎后將球放回抽獎箱.活動另附說明如下:
①凡購物滿100(含100)元者,憑購物打印憑條可獲得一次抽獎機會;
②凡購物滿188(含188)元者,憑購物打印憑條可獲得兩次抽獎機會;
③若取得的3個小球只有1種顏色,則該顧客中得一等獎,獎金是一個10元的紅包;
④若取得的3個小球有3種顏色,則該顧客中得二等獎,獎金是一個5元的紅包;
⑤若取得的3個小球只有2種顏色,則該顧客中得三等獎,獎金是一個2元的紅包.
抽獎活動的組織者記錄了該超市前20位顧客的購物消費數據(單位:元),繪制得到如圖所示的莖葉圖.

(1)求這20位顧客中獎得抽獎機會的顧客的購物消費數據的中位數與平均數(結果精確到整數部分);
(2)記一次抽獎獲得的紅包獎金數(單位:元)為![]() ,求
,求![]() 的分布列及數學期望,并計算這20位顧客(假定每位獲得抽獎機會的顧客都會去抽獎)在抽獎中獲得紅包的總獎金數的平均值.
的分布列及數學期望,并計算這20位顧客(假定每位獲得抽獎機會的顧客都會去抽獎)在抽獎中獲得紅包的總獎金數的平均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海中一小島![]() 的周圍
的周圍![]()
![]() 內有暗礁,海輪由西向東航行至
內有暗礁,海輪由西向東航行至![]() 處測得小島
處測得小島![]() 位于北偏東
位于北偏東![]() ,航行8
,航行8![]() 后,于
后,于![]() 處測得小島
處測得小島![]() 在北偏東
在北偏東![]() (如圖所示).
(如圖所示).

(1)如果這艘海輪不改變航向,有沒有觸礁的危險?請說明理由.
(2)如果有觸礁的危險,這艘海輪在![]() 處改變航向為東偏南
處改變航向為東偏南![]() (
(![]() )方向航行,求
)方向航行,求![]() 的最小值.
的最小值.
附: ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.
AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.

(I)在平面PAB內找一點M,使得直線CM∥平面PBE,并說明理由;
(II)若二面角P-CD-A的大小為45°,求直線PA與平面PCE所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com