
本題滿分16分)
如圖,拋物線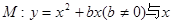 軸交于O,A兩點,交直線
軸交于O,A兩點,交直線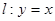 于O,B兩點,經(jīng)過三點O,A,B作圓C。
于O,B兩點,經(jīng)過三點O,A,B作圓C。
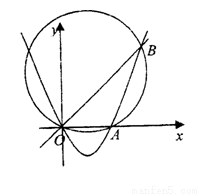
(I)求證:當(dāng)b變化時,圓C的圓心在一條定直線上;
(II)求證:圓C經(jīng)過除原點外的一個定點;
(III)是否存在這樣的拋物線M,使它的頂點與C的距離不大于圓C的半徑?
解:(I)易得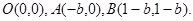
設(shè)圓C的方程為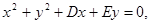
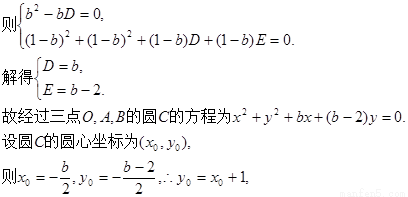 ………………4分
………………4分
這說明當(dāng)b變化時,(I)中的圓C的圓心在定直線 上。………………6分
上。………………6分
(II)設(shè)圓C過定點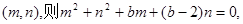
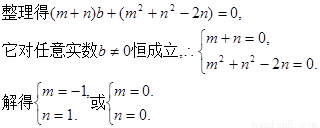 ………………9分
………………9分
故當(dāng)b變化時,(I)中的圓C經(jīng)過除原點外的一個定點坐標(biāo)為(—1,1)。11分
(III)拋物線M的頂點坐標(biāo)為(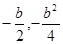 ),若存在這樣的拋物線M,使它的頂點與它對應(yīng)的圓C的圓心之間的距離不大于圓C的半徑,
),若存在這樣的拋物線M,使它的頂點與它對應(yīng)的圓C的圓心之間的距離不大于圓C的半徑,
則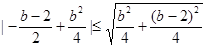 ,………………14分
,………………14分
整理得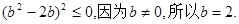
以上過程均可逆,故存在拋物線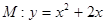 使它的頂點與C的距離不大于圓C的半徑。 ………………16分
使它的頂點與C的距離不大于圓C的半徑。 ………………16分
【解析】略


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案 應(yīng)用題作業(yè)本系列答案
應(yīng)用題作業(yè)本系列答案科目:高中數(shù)學(xué) 來源:2014屆江蘇省高二上學(xué)期期中考試數(shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分16分)如圖:AD=2,AB=4的長方形 所在平面與正
所在平面與正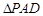 所在平面互相垂直,
所在平面互相垂直,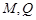 分別為
分別為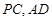 的中點.
的中點.
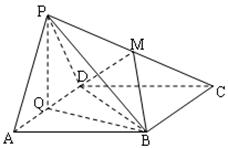
(1)求四棱錐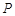 -
- 的體積;
的體積;
(2)求證: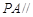 平面
平面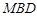 ;
;
(3)試問:在線段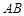 上是否存在一點
上是否存在一點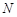 ,使得平面
,使得平面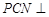 平面
平面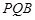 ?若存在,試指出點
?若存在,試指出點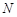 的位置,并證明你的結(jié)論;若不存在,請說明理由.
的位置,并證明你的結(jié)論;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆江蘇省高二9月份質(zhì)量檢測數(shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分16分)
如圖,橢圓C: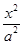 +
+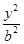 =1(a>b>0)的焦點F1,F(xiàn)2和短軸的一個端點A構(gòu)成等邊三角形,
=1(a>b>0)的焦點F1,F(xiàn)2和短軸的一個端點A構(gòu)成等邊三角形,
點(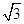 ,
,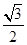 )在橢圓C上,直線l為橢圓C的左準(zhǔn)線.
)在橢圓C上,直線l為橢圓C的左準(zhǔn)線.
(1) 求橢圓C的方程;
(2) 點P是橢圓C上的動點,PQ ⊥l,垂足為Q.
是否存在點P,使得△F1PQ為等腰三角形?
若存在,求出點P的坐標(biāo);若不存在,說明理由.
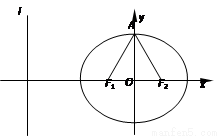
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年江蘇省無錫市高三上學(xué)期期中考試數(shù)學(xué)(解析版) 題型:解答題
(本題滿分16分)
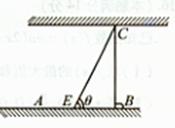
如圖為河岸一段的示意圖,一游泳者站在河岸的A點處,欲前往河對岸的C點處。若河寬BC為100m,A、B相距100m,他希望盡快到達(dá)C,準(zhǔn)備從A步行到E(E為河岸AB上的點),再從E游到C。已知此人步行速度為v,游泳速度為0.5v。
(I)設(shè)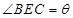 ,試將此人按上述路線從A到C所需時間T表示為
,試將此人按上述路線從A到C所需時間T表示為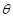 的函數(shù);并求自變量
的函數(shù);并求自變量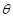 取值范圍;
取值范圍;
II)當(dāng)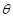 為何值時,此人從A經(jīng)E游到C所需時間T最小,其最小值是多少?
為何值時,此人從A經(jīng)E游到C所需時間T最小,其最小值是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013屆上海市高二年級期終考試數(shù)學(xué) 題型:解答題
(本題滿分16分)
如圖,在四棱錐 中,底面
中,底面 是矩形.已知
是矩形.已知 .
.
(1)證明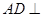 平面
平面 ;
;
(2)求異面直線 與
與 所成的角的大小;
所成的角的大小;
(3)求二面角 的大小.
的大小.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年新疆農(nóng)七師高級中學(xué)高一第二學(xué)期第二階段考試數(shù)學(xué)試題 題型:解答題
(本題滿分16分)如圖,已知點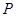 是正方形
是正方形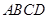 所在平面外一點,
所在平面外一點,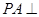 平面
平面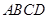 ,
,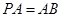 ,點
,點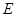 、
、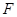 分別在線段
分別在線段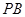 、
、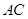 上,滿足
上,滿足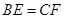 .
.
(1)求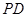 與平面
與平面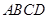 所成的角的大小;
所成的角的大小;
(2)求平面PBD與平面ABCD所成角的正切值。
(3)求證: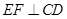 ;
;
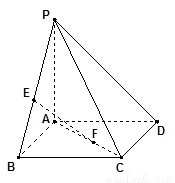
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com