
用反證法證明:“方程ax2+bx+c=0,且a,b,c都是奇數,則方程沒有整數根”正確的假設是方程存在實數根x0為( )
A.整數 B.奇數或偶數 C.正整數或負整數 D.自然數或負整數
科目:高中數學 來源:[同步]2014年新人教A版選修4-5 3.2一般形式柯西不等式練習卷(解析版) 題型:選擇題
(2012•湖北)設a,b,c,x,y,z是正數,且a2+b2+c2=10,x2+y2+z2=40,ax+by+cz=20,則 =( )
=( )
A.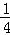 B.
B. C.
C. D.
D.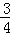
查看答案和解析>>
科目:高中數學 來源:[同步]2014年新人教A版選修4-5 3.1二維形式柯西不等式練習卷(解析版) 題型:選擇題
已知x2+4y2+kz2=36,且x+y+z的最大值為7,則正數k等于( )
A.1 B.4 C.8 D.9
查看答案和解析>>
科目:高中數學 來源:[同步]2014年新人教A版選修4-5 2.3反證法與放縮法練習卷(解析版) 題型:選擇題
用反證法證明:“a>b”,應假設為( )
A.a>b B.a<b C.a=b D.a≤b
查看答案和解析>>
科目:高中數學 來源:[同步]2014年新人教A版選修4-5 2.3反證法與放縮法練習卷(解析版) 題型:選擇題
用反證法證明命題“a,b∈N,如果ab可被5整除,那么a,b至少有1個能被5整除.”則假設的內容是( )
A.a,b都能被5整除 B.a,b都不能被5整除
C.a,b不能被5整除 D.a,b有1個不能被5整除
查看答案和解析>>
科目:高中數學 來源:[同步]2014年新人教A版選修4-5 2.3反證法與放縮法練習卷(解析版) 題型:選擇題
用反證法證明命題:“已知a,b為實數,則方程x2+ax+b=0至少有一個實根”時,要做的假設是( )
A.方程x2+ax+b=0沒有實根
B.方程x2+ax+b=0至多有一個實根
C.方程x2+ax+b=0至多有兩個實根
D.方程x2+ax+b=0恰好有兩個實根
查看答案和解析>>
科目:高中數學 來源:[同步]2014年新人教A版選修4-5 2.2綜合法與分析法練習卷(解析版) 題型:選擇題
關于綜合法和分析法說法錯誤的是( )
A.綜合法和分析法是直接證明中最基本的兩種證明方法
B.綜合法又叫順推證法或由因導果法
C.分析法又叫逆推證法或執果索因法
D.綜合法和分析法都是因果分別互推的兩頭湊法
查看答案和解析>>
科目:高中數學 來源:[同步]2014年新人教A版選修4-5 1.2絕對值不等式練習卷(解析版) 題型:選擇題
(2014•江西二模)若存在x∈R,使|2x﹣a|+2|3﹣x|≤1成立,則實數a的取值范圍是( )
A.[2,4] B.(5,7) C.[5,7] D.(﹣∞,5]∪[7,+∞)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com